Continuando con la serie sobre cosas de inferencia causal y full luxury bayes, antes de que empiece mi amigo Carlos Gil, y dónde seguramente se aprenderá más.
Este ejemplo viene motivado precisamente por una charla que tuve el otro día con él.
Sea el siguiente diagrama causal
library(tidyverse)
library(dagitty)
library(ggdag)
g <- dagitty("dag{
x -> y ;
z -> y ;
x -> z
}")
ggdag(g) 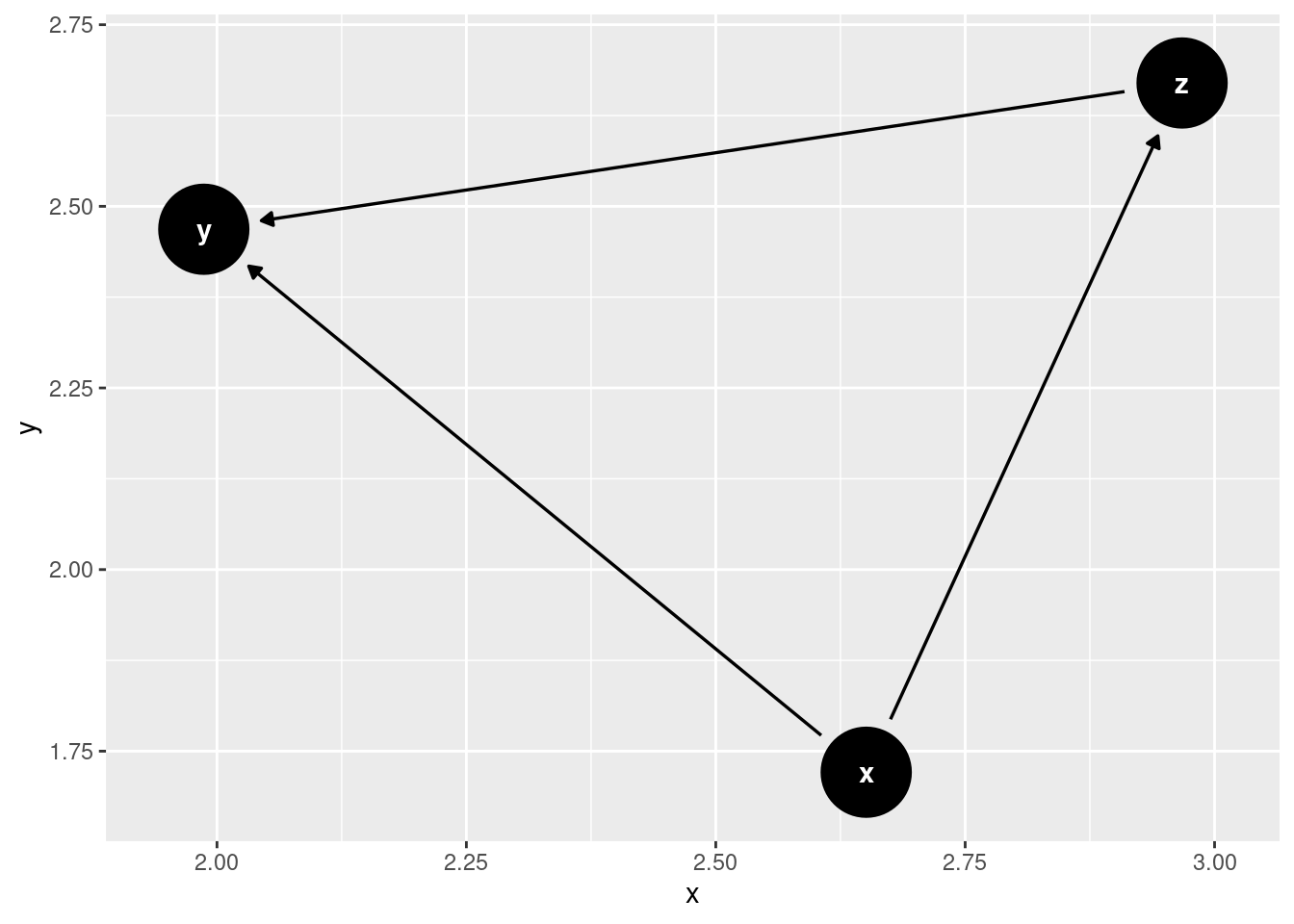
Se tiene que z es un mediador entre x e y, y la teoría nos dice que si quiero obtener el efecto directo de x sobre y he de condicionar por z , y efectivamente, así nos lo dice el backdoor criterio. Mientras que si quiero el efecto total de x sobre y no he de condicionar por z.
adjustmentSets(g, exposure = "x", outcome = "y", effect = "total" )## {} adjustmentSets(g, exposure = "x", outcome = "y", effect = "direct" )## { z }Datos simulados
set.seed(155)
N <- 1000
x <- rnorm(N, 2, 1)
z <- rnorm(N, 4+ 4*x , 2 ) # a z le ponemos más variabilidad, pero daría igual
y <- rnorm(N, 2+ 3*x + z, 1)Efecto total de x sobre y
Tal y como hemos simulado los datos, se esperaría que el efecto total de x sobre y fuera
\[ \dfrac{cov(x,y)} {var(x)} \approx 7 \]
Y qué el efecto directo fuera de 3
Efectivamente
Efecto total
# efecto total
lm(y~x)##
## Call:
## lm(formula = y ~ x)
##
## Coefficients:
## (Intercept) x
## 5.881 7.112# efecto directo
lm(y~x+z)##
## Call:
## lm(formula = y ~ x + z)
##
## Coefficients:
## (Intercept) x z
## 2.0318 3.0339 0.9945Full luxury bayes
Hagamos lo mismo pero estimando el dag completo
library(cmdstanr)
library(rethinking)
set_cmdstan_path("~/Descargas/cmdstan/")
dat <- list(
N = N,
x = x,
y = y,
z = z
)
set.seed(1908)
flbi <- ulam(
alist(
# x model, si quiero estimar la media de x sino, no me hace falta
x ~ normal(mux, k),
mux <- a0,
z ~ normal( mu , sigma ),
mu <- a1 + bx * x,
y ~ normal( nu , tau ),
nu <- a2 + bx2 * x + bz * z,
# priors
c(a0,a1,a2,bx,bx2, bz) ~ normal( 0 , 0.5 ),
c(sigma,tau, k) ~ exponential( 1 )
), data=dat , chains=10 , cores=10 , warmup = 500, iter=2000 , cmdstan=TRUE )## Running MCMC with 10 parallel chains, with 1 thread(s) per chain...
##
## Chain 1 Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 2 Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 3 Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 3 Iteration: 100 / 2000 [ 5%] (Warmup)
## Chain 4 Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 5 Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 6 Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 7 Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 8 Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 9 Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 10 Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 1 Iteration: 100 / 2000 [ 5%] (Warmup)
## Chain 4 Iteration: 100 / 2000 [ 5%] (Warmup)
## Chain 8 Iteration: 100 / 2000 [ 5%] (Warmup)
## Chain 9 Iteration: 100 / 2000 [ 5%] (Warmup)
## Chain 7 Iteration: 100 / 2000 [ 5%] (Warmup)
## Chain 5 Iteration: 100 / 2000 [ 5%] (Warmup)
## Chain 10 Iteration: 100 / 2000 [ 5%] (Warmup)
## Chain 2 Iteration: 100 / 2000 [ 5%] (Warmup)
## Chain 6 Iteration: 100 / 2000 [ 5%] (Warmup)
## Chain 9 Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 1 Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 3 Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 5 Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 4 Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 8 Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 7 Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 10 Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 2 Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 6 Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 9 Iteration: 300 / 2000 [ 15%] (Warmup)
## Chain 1 Iteration: 300 / 2000 [ 15%] (Warmup)
## Chain 5 Iteration: 300 / 2000 [ 15%] (Warmup)
## Chain 10 Iteration: 300 / 2000 [ 15%] (Warmup)
## Chain 3 Iteration: 300 / 2000 [ 15%] (Warmup)
## Chain 2 Iteration: 300 / 2000 [ 15%] (Warmup)
## Chain 4 Iteration: 300 / 2000 [ 15%] (Warmup)
## Chain 8 Iteration: 300 / 2000 [ 15%] (Warmup)
## Chain 7 Iteration: 300 / 2000 [ 15%] (Warmup)
## Chain 9 Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 6 Iteration: 300 / 2000 [ 15%] (Warmup)
## Chain 1 Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 10 Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 2 Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 4 Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 5 Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 3 Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 8 Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 7 Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 9 Iteration: 500 / 2000 [ 25%] (Warmup)
## Chain 9 Iteration: 501 / 2000 [ 25%] (Sampling)
## Chain 6 Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 4 Iteration: 500 / 2000 [ 25%] (Warmup)
## Chain 4 Iteration: 501 / 2000 [ 25%] (Sampling)
## Chain 5 Iteration: 500 / 2000 [ 25%] (Warmup)
## Chain 5 Iteration: 501 / 2000 [ 25%] (Sampling)
## Chain 1 Iteration: 500 / 2000 [ 25%] (Warmup)
## Chain 1 Iteration: 501 / 2000 [ 25%] (Sampling)
## Chain 10 Iteration: 500 / 2000 [ 25%] (Warmup)
## Chain 10 Iteration: 501 / 2000 [ 25%] (Sampling)
## Chain 3 Iteration: 500 / 2000 [ 25%] (Warmup)
## Chain 3 Iteration: 501 / 2000 [ 25%] (Sampling)
## Chain 2 Iteration: 500 / 2000 [ 25%] (Warmup)
## Chain 2 Iteration: 501 / 2000 [ 25%] (Sampling)
## Chain 8 Iteration: 500 / 2000 [ 25%] (Warmup)
## Chain 8 Iteration: 501 / 2000 [ 25%] (Sampling)
## Chain 9 Iteration: 600 / 2000 [ 30%] (Sampling)
## Chain 7 Iteration: 500 / 2000 [ 25%] (Warmup)
## Chain 7 Iteration: 501 / 2000 [ 25%] (Sampling)
## Chain 5 Iteration: 600 / 2000 [ 30%] (Sampling)
## Chain 6 Iteration: 500 / 2000 [ 25%] (Warmup)
## Chain 6 Iteration: 501 / 2000 [ 25%] (Sampling)
## Chain 1 Iteration: 600 / 2000 [ 30%] (Sampling)
## Chain 2 Iteration: 600 / 2000 [ 30%] (Sampling)
## Chain 4 Iteration: 600 / 2000 [ 30%] (Sampling)
## Chain 8 Iteration: 600 / 2000 [ 30%] (Sampling)
## Chain 3 Iteration: 600 / 2000 [ 30%] (Sampling)
## Chain 10 Iteration: 600 / 2000 [ 30%] (Sampling)
## Chain 9 Iteration: 700 / 2000 [ 35%] (Sampling)
## Chain 6 Iteration: 600 / 2000 [ 30%] (Sampling)
## Chain 1 Iteration: 700 / 2000 [ 35%] (Sampling)
## Chain 7 Iteration: 600 / 2000 [ 30%] (Sampling)
## Chain 8 Iteration: 700 / 2000 [ 35%] (Sampling)
## Chain 5 Iteration: 700 / 2000 [ 35%] (Sampling)
## Chain 2 Iteration: 700 / 2000 [ 35%] (Sampling)
## Chain 3 Iteration: 700 / 2000 [ 35%] (Sampling)
## Chain 4 Iteration: 700 / 2000 [ 35%] (Sampling)
## Chain 8 Iteration: 800 / 2000 [ 40%] (Sampling)
## Chain 9 Iteration: 800 / 2000 [ 40%] (Sampling)
## Chain 10 Iteration: 700 / 2000 [ 35%] (Sampling)
## Chain 6 Iteration: 700 / 2000 [ 35%] (Sampling)
## Chain 1 Iteration: 800 / 2000 [ 40%] (Sampling)
## Chain 5 Iteration: 800 / 2000 [ 40%] (Sampling)
## Chain 2 Iteration: 800 / 2000 [ 40%] (Sampling)
## Chain 7 Iteration: 700 / 2000 [ 35%] (Sampling)
## Chain 3 Iteration: 800 / 2000 [ 40%] (Sampling)
## Chain 8 Iteration: 900 / 2000 [ 45%] (Sampling)
## Chain 4 Iteration: 800 / 2000 [ 40%] (Sampling)
## Chain 9 Iteration: 900 / 2000 [ 45%] (Sampling)
## Chain 6 Iteration: 800 / 2000 [ 40%] (Sampling)
## Chain 1 Iteration: 900 / 2000 [ 45%] (Sampling)
## Chain 10 Iteration: 800 / 2000 [ 40%] (Sampling)
## Chain 2 Iteration: 900 / 2000 [ 45%] (Sampling)
## Chain 5 Iteration: 900 / 2000 [ 45%] (Sampling)
## Chain 8 Iteration: 1000 / 2000 [ 50%] (Sampling)
## Chain 7 Iteration: 800 / 2000 [ 40%] (Sampling)
## Chain 3 Iteration: 900 / 2000 [ 45%] (Sampling)
## Chain 9 Iteration: 1000 / 2000 [ 50%] (Sampling)
## Chain 6 Iteration: 900 / 2000 [ 45%] (Sampling)
## Chain 4 Iteration: 900 / 2000 [ 45%] (Sampling)
## Chain 1 Iteration: 1000 / 2000 [ 50%] (Sampling)
## Chain 8 Iteration: 1100 / 2000 [ 55%] (Sampling)
## Chain 10 Iteration: 900 / 2000 [ 45%] (Sampling)
## Chain 9 Iteration: 1100 / 2000 [ 55%] (Sampling)
## Chain 2 Iteration: 1000 / 2000 [ 50%] (Sampling)
## Chain 5 Iteration: 1000 / 2000 [ 50%] (Sampling)
## Chain 3 Iteration: 1000 / 2000 [ 50%] (Sampling)
## Chain 6 Iteration: 1000 / 2000 [ 50%] (Sampling)
## Chain 7 Iteration: 900 / 2000 [ 45%] (Sampling)
## Chain 8 Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 1 Iteration: 1100 / 2000 [ 55%] (Sampling)
## Chain 4 Iteration: 1000 / 2000 [ 50%] (Sampling)
## Chain 9 Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 10 Iteration: 1000 / 2000 [ 50%] (Sampling)
## Chain 2 Iteration: 1100 / 2000 [ 55%] (Sampling)
## Chain 6 Iteration: 1100 / 2000 [ 55%] (Sampling)
## Chain 3 Iteration: 1100 / 2000 [ 55%] (Sampling)
## Chain 5 Iteration: 1100 / 2000 [ 55%] (Sampling)
## Chain 8 Iteration: 1300 / 2000 [ 65%] (Sampling)
## Chain 7 Iteration: 1000 / 2000 [ 50%] (Sampling)
## Chain 9 Iteration: 1300 / 2000 [ 65%] (Sampling)
## Chain 1 Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 4 Iteration: 1100 / 2000 [ 55%] (Sampling)
## Chain 6 Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 10 Iteration: 1100 / 2000 [ 55%] (Sampling)
## Chain 2 Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 3 Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 8 Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 5 Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 7 Iteration: 1100 / 2000 [ 55%] (Sampling)
## Chain 1 Iteration: 1300 / 2000 [ 65%] (Sampling)
## Chain 6 Iteration: 1300 / 2000 [ 65%] (Sampling)
## Chain 9 Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 2 Iteration: 1300 / 2000 [ 65%] (Sampling)
## Chain 4 Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 8 Iteration: 1500 / 2000 [ 75%] (Sampling)
## Chain 3 Iteration: 1300 / 2000 [ 65%] (Sampling)
## Chain 10 Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 5 Iteration: 1300 / 2000 [ 65%] (Sampling)
## Chain 6 Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 7 Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 9 Iteration: 1500 / 2000 [ 75%] (Sampling)
## Chain 1 Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 8 Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 2 Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 3 Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 5 Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 4 Iteration: 1300 / 2000 [ 65%] (Sampling)
## Chain 6 Iteration: 1500 / 2000 [ 75%] (Sampling)
## Chain 9 Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 10 Iteration: 1300 / 2000 [ 65%] (Sampling)
## Chain 8 Iteration: 1700 / 2000 [ 85%] (Sampling)
## Chain 1 Iteration: 1500 / 2000 [ 75%] (Sampling)
## Chain 7 Iteration: 1300 / 2000 [ 65%] (Sampling)
## Chain 2 Iteration: 1500 / 2000 [ 75%] (Sampling)
## Chain 3 Iteration: 1500 / 2000 [ 75%] (Sampling)
## Chain 5 Iteration: 1500 / 2000 [ 75%] (Sampling)
## Chain 4 Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 8 Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 6 Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 9 Iteration: 1700 / 2000 [ 85%] (Sampling)
## Chain 1 Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 10 Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 7 Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 2 Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 3 Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 5 Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 8 Iteration: 1900 / 2000 [ 95%] (Sampling)
## Chain 6 Iteration: 1700 / 2000 [ 85%] (Sampling)
## Chain 1 Iteration: 1700 / 2000 [ 85%] (Sampling)
## Chain 4 Iteration: 1500 / 2000 [ 75%] (Sampling)
## Chain 9 Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 10 Iteration: 1500 / 2000 [ 75%] (Sampling)
## Chain 8 Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 8 finished in 26.1 seconds.
## Chain 2 Iteration: 1700 / 2000 [ 85%] (Sampling)
## Chain 3 Iteration: 1700 / 2000 [ 85%] (Sampling)
## Chain 7 Iteration: 1500 / 2000 [ 75%] (Sampling)
## Chain 1 Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 5 Iteration: 1700 / 2000 [ 85%] (Sampling)
## Chain 6 Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 9 Iteration: 1900 / 2000 [ 95%] (Sampling)
## Chain 4 Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 6 Iteration: 1900 / 2000 [ 95%] (Sampling)
## Chain 1 Iteration: 1900 / 2000 [ 95%] (Sampling)
## Chain 10 Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 3 Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 2 Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 7 Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 5 Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 6 Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 6 finished in 28.2 seconds.
## Chain 9 Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 9 finished in 28.3 seconds.
## Chain 10 Iteration: 1700 / 2000 [ 85%] (Sampling)
## Chain 1 Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 1 finished in 28.9 seconds.
## Chain 3 Iteration: 1900 / 2000 [ 95%] (Sampling)
## Chain 4 Iteration: 1700 / 2000 [ 85%] (Sampling)
## Chain 5 Iteration: 1900 / 2000 [ 95%] (Sampling)
## Chain 2 Iteration: 1900 / 2000 [ 95%] (Sampling)
## Chain 7 Iteration: 1700 / 2000 [ 85%] (Sampling)
## Chain 10 Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 3 Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 5 Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 3 finished in 30.0 seconds.
## Chain 5 finished in 29.9 seconds.
## Chain 2 Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 2 finished in 30.2 seconds.
## Chain 4 Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 7 Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 10 Iteration: 1900 / 2000 [ 95%] (Sampling)
## Chain 4 Iteration: 1900 / 2000 [ 95%] (Sampling)
## Chain 7 Iteration: 1900 / 2000 [ 95%] (Sampling)
## Chain 10 Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 10 finished in 31.6 seconds.
## Chain 4 Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 4 finished in 32.6 seconds.
## Chain 7 Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 7 finished in 32.7 seconds.
##
## All 10 chains finished successfully.
## Mean chain execution time: 29.8 seconds.
## Total execution time: 33.0 seconds.Y recuperamos los coeficientes y varianzas
precis(flbi)## mean sd 5.5% 94.5% n_eff Rhat4
## bz 1.0131931 0.01557219 0.9883466 1.038241 8226.042 1.0005919
## bx2 2.9610334 0.07098661 2.8447278 3.073501 9640.122 1.0004040
## bx 4.1535508 0.06180592 4.0552767 4.252771 8753.661 1.0001456
## a2 1.9440850 0.09315785 1.7952495 2.093027 11266.267 1.0001373
## a1 3.7089914 0.13578637 3.4916007 3.926010 8709.448 1.0002893
## a0 1.9857103 0.03108199 1.9357773 2.035712 16252.310 0.9997523
## k 0.9719412 0.02166791 0.9378896 1.007410 15276.158 0.9999036
## tau 0.9859183 0.02216068 0.9512944 1.021932 15735.140 1.0001540
## sigma 1.9636543 0.04382554 1.8950489 2.034130 15855.098 1.0000898# extraemos 10000 muestras de la posteriori
post <- extract.samples(flbi, n = 10000) Y el efecto directo de x sobre y sería
quantile(post$bx2, probs = c(0.025, 0.5, 0.975))## 2.5% 50% 97.5%
## 2.823659 2.962330 3.099855En este ejemplo sencillo, podríamos estimar el efecto causal de x sobre y simplemente sumando las posterioris
quantile(post$bx + post$bx2, c(0.025, 0.5, 0.975))## 2.5% 50% 97.5%
## 6.928046 7.114180 7.299252También podríamos obtener el efecto causal total de x sobre y simulando una intervención. En este caso, al ser la variable continua, lo que queremos obtener como de diferente es y cuando \(X = x_i\) versus cuando \(X = x_i+1\).
Siempre podríamos ajustar otro modelo bayesiano dónde no tuviéramos en cuenta a z y obtendríamos la estimación de ese efecto total de x sobre y, pero siguiendo a Rubin y Gelman, la idea es incluir en nuestro modelo toda la información disponible. Y tal y como dice Richard McElreath , Statistical Rethinking 2022, el efecto causal se puede estimar simulando la intervención.
Así que el objetivo es dado nuestro modelo que incluye la variable z, simular la intervención cuando \(X = x_i\) y cuando \(X = x_i+1\) y una estimación del efecto directo es la resta de ambas distribuciones a posteriori de y.
Creamos función para calcular el efecto de la intervención y_do_x
get_total_effect <- function(x_value = 0, incremento = 0.5) {
n <- length(post$bx)
with(post, {
# simulate z, y for x= x_value
z_x0 <- rnorm(n, a1 + bx * x_value , sigma)
y_x0 <- rnorm(n, a2 + bz * z_x0 + bx * x_value , tau)
# simulate z,y for x= x_value +1
z_x1 <- rnorm(n, a1 + bx * (x_value + incremento) , sigma)
y_x1 <- rnorm(n, a2 + bz * z_x1 + bx2 * (x_value + incremento) , tau)
# compute contrast
y_do_x <- (y_x1 - y_x0) / incremento
return(y_do_x)
})
}Dado un valor de x, podemos calcular el efecto total
y_do_x_0_2 <- get_total_effect(x_value = 0.2)
quantile(y_do_x_0_2)## 0% 25% 50% 75% 100%
## -15.324628 2.395551 6.702379 10.987520 28.909002Podríamos hacer lo mismo para varios valores de x
x_seq <- seq(-0.5, 0.5, length = 1000)
y_do_x <-
mclapply(x_seq, function(lambda)
get_total_effect(x_value = lambda))Y para cada uno de estos 1000 valores tendría 10000 valores de su efecto total de x sobre y.
length(y_do_x[[500]])## [1] 10000head(y_do_x[[500]])## [1] 3.772497 4.714584 -4.278250 18.685830 10.009083 9.922863Calculamos los intervalos de credibilidad del efecto total de x sobre y para cada valor de x.
# lo hacemos simplemente por cuantiles, aunque podríamos calcular el hdi también,
intervalos_credibilidad <- mclapply( y_do_x, function(x) quantile(x, probs = c(0.025, 0.5, 0.975)))
# Media e intervalor de credibilidad para el valor de x_seq en la posición 500
mean(y_do_x[[500]])## [1] 7.174111intervalos_credibilidad[[500]]## 2.5% 50% 97.5%
## -5.143874 7.156823 19.337530intervalo de predicción clásico con el lm
Habría que calcular la predicción de y para un valor de x y para el de x + 1, podemos calcular los intervalos de predicción clásicos parea cada valor de x, pero no para la diferencia ( al menos con la función predict)
mt_lm <- lm(y~x)
predict(mt_lm, newdata = list(x= x_seq[[500]]), interval = "prediction")## fit lwr upr
## 1 5.877439 1.578777 10.1761predict(mt_lm, newdata = list(x= x_seq[[500]] +1), interval = "prediction")## fit lwr upr
## 1 12.98993 8.698051 17.2818Pero como sería obtener el intervalo de credibilidad para la media de los efectos totales?
Calculando para cada valor de x la media de la posteriori del efecto global y juntando todas las medias.
slopes_mean <- lapply(y_do_x, mean)
quantile(unlist(slopes_mean), c(0.025, 0.5, 0.975))## 2.5% 50% 97.5%
## 6.034370 7.166049 8.303448Que tiene mucha menos variabilidad que el efecto global en un valor concreto de x, o si juntamos todas las estimaciones
quantile(unlist(y_do_x), c(0.025, 0.5, 0.975))## 2.5% 50% 97.5%
## -5.218662 7.169611 19.559376Evidentemente, podríamos simplemente no haber tenido en cuenta la variable z en nuestro modelo bayesiano.
flbi_2 <- ulam(
alist(
# x model, si quiero estimar la media de x sino, no me hace falta
x ~ normal(mux, k),
mux <- a1,
y ~ normal( nu , tau ),
nu <- a2 + bx * x ,
# priors
c(a1,a2,bx) ~ normal( 0 , 0.5 ),
c(tau, k) ~ exponential( 1 )
), data=dat , chains=10 , cores=10 , warmup = 500, iter=2000 , cmdstan=TRUE )## Running MCMC with 10 parallel chains, with 1 thread(s) per chain...
##
## Chain 1 Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 1 Iteration: 100 / 2000 [ 5%] (Warmup)
## Chain 1 Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 1 Iteration: 300 / 2000 [ 15%] (Warmup)
## Chain 2 Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 2 Iteration: 100 / 2000 [ 5%] (Warmup)
## Chain 2 Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 2 Iteration: 300 / 2000 [ 15%] (Warmup)
## Chain 3 Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 3 Iteration: 100 / 2000 [ 5%] (Warmup)
## Chain 4 Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 4 Iteration: 100 / 2000 [ 5%] (Warmup)
## Chain 5 Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 5 Iteration: 100 / 2000 [ 5%] (Warmup)
## Chain 5 Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 5 Iteration: 300 / 2000 [ 15%] (Warmup)
## Chain 6 Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 6 Iteration: 100 / 2000 [ 5%] (Warmup)
## Chain 7 Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 7 Iteration: 100 / 2000 [ 5%] (Warmup)
## Chain 7 Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 8 Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 8 Iteration: 100 / 2000 [ 5%] (Warmup)
## Chain 8 Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 9 Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 9 Iteration: 100 / 2000 [ 5%] (Warmup)
## Chain 9 Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 10 Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 10 Iteration: 100 / 2000 [ 5%] (Warmup)
## Chain 1 Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 1 Iteration: 500 / 2000 [ 25%] (Warmup)
## Chain 1 Iteration: 501 / 2000 [ 25%] (Sampling)
## Chain 2 Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 2 Iteration: 500 / 2000 [ 25%] (Warmup)
## Chain 2 Iteration: 501 / 2000 [ 25%] (Sampling)
## Chain 3 Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 3 Iteration: 300 / 2000 [ 15%] (Warmup)
## Chain 4 Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 5 Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 7 Iteration: 300 / 2000 [ 15%] (Warmup)
## Chain 2 Iteration: 600 / 2000 [ 30%] (Sampling)
## Chain 5 Iteration: 500 / 2000 [ 25%] (Warmup)
## Chain 5 Iteration: 501 / 2000 [ 25%] (Sampling)
## Chain 8 Iteration: 300 / 2000 [ 15%] (Warmup)
## Chain 9 Iteration: 300 / 2000 [ 15%] (Warmup)
## Chain 10 Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 1 Iteration: 600 / 2000 [ 30%] (Sampling)
## Chain 2 Iteration: 700 / 2000 [ 35%] (Sampling)
## Chain 3 Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 6 Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 7 Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 4 Iteration: 300 / 2000 [ 15%] (Warmup)
## Chain 5 Iteration: 600 / 2000 [ 30%] (Sampling)
## Chain 8 Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 9 Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 1 Iteration: 700 / 2000 [ 35%] (Sampling)
## Chain 2 Iteration: 800 / 2000 [ 40%] (Sampling)
## Chain 3 Iteration: 500 / 2000 [ 25%] (Warmup)
## Chain 3 Iteration: 501 / 2000 [ 25%] (Sampling)
## Chain 10 Iteration: 300 / 2000 [ 15%] (Warmup)
## Chain 1 Iteration: 800 / 2000 [ 40%] (Sampling)
## Chain 2 Iteration: 900 / 2000 [ 45%] (Sampling)
## Chain 3 Iteration: 600 / 2000 [ 30%] (Sampling)
## Chain 4 Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 5 Iteration: 700 / 2000 [ 35%] (Sampling)
## Chain 6 Iteration: 300 / 2000 [ 15%] (Warmup)
## Chain 7 Iteration: 500 / 2000 [ 25%] (Warmup)
## Chain 7 Iteration: 501 / 2000 [ 25%] (Sampling)
## Chain 9 Iteration: 500 / 2000 [ 25%] (Warmup)
## Chain 9 Iteration: 501 / 2000 [ 25%] (Sampling)
## Chain 8 Iteration: 500 / 2000 [ 25%] (Warmup)
## Chain 8 Iteration: 501 / 2000 [ 25%] (Sampling)
## Chain 10 Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 1 Iteration: 900 / 2000 [ 45%] (Sampling)
## Chain 2 Iteration: 1000 / 2000 [ 50%] (Sampling)
## Chain 3 Iteration: 700 / 2000 [ 35%] (Sampling)
## Chain 4 Iteration: 500 / 2000 [ 25%] (Warmup)
## Chain 4 Iteration: 501 / 2000 [ 25%] (Sampling)
## Chain 5 Iteration: 800 / 2000 [ 40%] (Sampling)
## Chain 6 Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 7 Iteration: 600 / 2000 [ 30%] (Sampling)
## Chain 9 Iteration: 600 / 2000 [ 30%] (Sampling)
## Chain 1 Iteration: 1000 / 2000 [ 50%] (Sampling)
## Chain 2 Iteration: 1100 / 2000 [ 55%] (Sampling)
## Chain 4 Iteration: 600 / 2000 [ 30%] (Sampling)
## Chain 5 Iteration: 900 / 2000 [ 45%] (Sampling)
## Chain 6 Iteration: 500 / 2000 [ 25%] (Warmup)
## Chain 6 Iteration: 501 / 2000 [ 25%] (Sampling)
## Chain 8 Iteration: 600 / 2000 [ 30%] (Sampling)
## Chain 9 Iteration: 700 / 2000 [ 35%] (Sampling)
## Chain 10 Iteration: 500 / 2000 [ 25%] (Warmup)
## Chain 10 Iteration: 501 / 2000 [ 25%] (Sampling)
## Chain 2 Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 3 Iteration: 800 / 2000 [ 40%] (Sampling)
## Chain 7 Iteration: 700 / 2000 [ 35%] (Sampling)
## Chain 8 Iteration: 700 / 2000 [ 35%] (Sampling)
## Chain 10 Iteration: 600 / 2000 [ 30%] (Sampling)
## Chain 1 Iteration: 1100 / 2000 [ 55%] (Sampling)
## Chain 2 Iteration: 1300 / 2000 [ 65%] (Sampling)
## Chain 3 Iteration: 900 / 2000 [ 45%] (Sampling)
## Chain 4 Iteration: 700 / 2000 [ 35%] (Sampling)
## Chain 5 Iteration: 1000 / 2000 [ 50%] (Sampling)
## Chain 6 Iteration: 600 / 2000 [ 30%] (Sampling)
## Chain 7 Iteration: 800 / 2000 [ 40%] (Sampling)
## Chain 9 Iteration: 800 / 2000 [ 40%] (Sampling)
## Chain 1 Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 2 Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 3 Iteration: 1000 / 2000 [ 50%] (Sampling)
## Chain 5 Iteration: 1100 / 2000 [ 55%] (Sampling)
## Chain 6 Iteration: 700 / 2000 [ 35%] (Sampling)
## Chain 8 Iteration: 800 / 2000 [ 40%] (Sampling)
## Chain 9 Iteration: 900 / 2000 [ 45%] (Sampling)
## Chain 10 Iteration: 700 / 2000 [ 35%] (Sampling)
## Chain 2 Iteration: 1500 / 2000 [ 75%] (Sampling)
## Chain 4 Iteration: 800 / 2000 [ 40%] (Sampling)
## Chain 6 Iteration: 800 / 2000 [ 40%] (Sampling)
## Chain 7 Iteration: 900 / 2000 [ 45%] (Sampling)
## Chain 8 Iteration: 900 / 2000 [ 45%] (Sampling)
## Chain 10 Iteration: 800 / 2000 [ 40%] (Sampling)
## Chain 1 Iteration: 1300 / 2000 [ 65%] (Sampling)
## Chain 2 Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 3 Iteration: 1100 / 2000 [ 55%] (Sampling)
## Chain 4 Iteration: 900 / 2000 [ 45%] (Sampling)
## Chain 5 Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 9 Iteration: 1000 / 2000 [ 50%] (Sampling)
## Chain 1 Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 2 Iteration: 1700 / 2000 [ 85%] (Sampling)
## Chain 3 Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 4 Iteration: 1000 / 2000 [ 50%] (Sampling)
## Chain 5 Iteration: 1300 / 2000 [ 65%] (Sampling)
## Chain 6 Iteration: 900 / 2000 [ 45%] (Sampling)
## Chain 7 Iteration: 1000 / 2000 [ 50%] (Sampling)
## Chain 8 Iteration: 1000 / 2000 [ 50%] (Sampling)
## Chain 9 Iteration: 1100 / 2000 [ 55%] (Sampling)
## Chain 10 Iteration: 900 / 2000 [ 45%] (Sampling)
## Chain 6 Iteration: 1000 / 2000 [ 50%] (Sampling)
## Chain 8 Iteration: 1100 / 2000 [ 55%] (Sampling)
## Chain 10 Iteration: 1000 / 2000 [ 50%] (Sampling)
## Chain 1 Iteration: 1500 / 2000 [ 75%] (Sampling)
## Chain 2 Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 3 Iteration: 1300 / 2000 [ 65%] (Sampling)
## Chain 4 Iteration: 1100 / 2000 [ 55%] (Sampling)
## Chain 5 Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 6 Iteration: 1100 / 2000 [ 55%] (Sampling)
## Chain 7 Iteration: 1100 / 2000 [ 55%] (Sampling)
## Chain 9 Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 1 Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 2 Iteration: 1900 / 2000 [ 95%] (Sampling)
## Chain 3 Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 4 Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 8 Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 9 Iteration: 1300 / 2000 [ 65%] (Sampling)
## Chain 10 Iteration: 1100 / 2000 [ 55%] (Sampling)
## Chain 2 Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 3 Iteration: 1500 / 2000 [ 75%] (Sampling)
## Chain 5 Iteration: 1500 / 2000 [ 75%] (Sampling)
## Chain 6 Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 7 Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 8 Iteration: 1300 / 2000 [ 65%] (Sampling)
## Chain 10 Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 2 finished in 2.7 seconds.
## Chain 1 Iteration: 1700 / 2000 [ 85%] (Sampling)
## Chain 4 Iteration: 1300 / 2000 [ 65%] (Sampling)
## Chain 5 Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 6 Iteration: 1300 / 2000 [ 65%] (Sampling)
## Chain 7 Iteration: 1300 / 2000 [ 65%] (Sampling)
## Chain 9 Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 1 Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 3 Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 4 Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 6 Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 8 Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 9 Iteration: 1500 / 2000 [ 75%] (Sampling)
## Chain 10 Iteration: 1300 / 2000 [ 65%] (Sampling)
## Chain 3 Iteration: 1700 / 2000 [ 85%] (Sampling)
## Chain 5 Iteration: 1700 / 2000 [ 85%] (Sampling)
## Chain 6 Iteration: 1500 / 2000 [ 75%] (Sampling)
## Chain 7 Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 8 Iteration: 1500 / 2000 [ 75%] (Sampling)
## Chain 10 Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 1 Iteration: 1900 / 2000 [ 95%] (Sampling)
## Chain 4 Iteration: 1500 / 2000 [ 75%] (Sampling)
## Chain 6 Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 9 Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 3 Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 4 Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 5 Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 6 Iteration: 1700 / 2000 [ 85%] (Sampling)
## Chain 7 Iteration: 1500 / 2000 [ 75%] (Sampling)
## Chain 8 Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 9 Iteration: 1700 / 2000 [ 85%] (Sampling)
## Chain 10 Iteration: 1500 / 2000 [ 75%] (Sampling)
## Chain 1 Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 3 Iteration: 1900 / 2000 [ 95%] (Sampling)
## Chain 5 Iteration: 1900 / 2000 [ 95%] (Sampling)
## Chain 1 finished in 3.3 seconds.
## Chain 6 Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 8 Iteration: 1700 / 2000 [ 85%] (Sampling)
## Chain 9 Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 10 Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 3 Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 4 Iteration: 1700 / 2000 [ 85%] (Sampling)
## Chain 5 Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 6 Iteration: 1900 / 2000 [ 95%] (Sampling)
## Chain 7 Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 8 Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 10 Iteration: 1700 / 2000 [ 85%] (Sampling)
## Chain 3 finished in 3.5 seconds.
## Chain 5 finished in 3.5 seconds.
## Chain 4 Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 7 Iteration: 1700 / 2000 [ 85%] (Sampling)
## Chain 9 Iteration: 1900 / 2000 [ 95%] (Sampling)
## Chain 4 Iteration: 1900 / 2000 [ 95%] (Sampling)
## Chain 6 Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 7 Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 8 Iteration: 1900 / 2000 [ 95%] (Sampling)
## Chain 9 Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 10 Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 10 Iteration: 1900 / 2000 [ 95%] (Sampling)
## Chain 6 finished in 3.7 seconds.
## Chain 9 finished in 3.6 seconds.
## Chain 4 Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 7 Iteration: 1900 / 2000 [ 95%] (Sampling)
## Chain 8 Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 10 Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 4 finished in 3.8 seconds.
## Chain 8 finished in 3.7 seconds.
## Chain 10 finished in 3.7 seconds.
## Chain 7 Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 7 finished in 3.9 seconds.
##
## All 10 chains finished successfully.
## Mean chain execution time: 3.5 seconds.
## Total execution time: 4.1 seconds.Y obtenemos directamente el efecto total de x sobre y.
precis(flbi_2)## mean sd 5.5% 94.5% n_eff Rhat4
## bx 7.1948083 0.06787458 7.0863389 7.302933 10446.14 1.0001211
## a2 5.6085615 0.14948341 5.3685467 5.848723 10598.69 1.0001680
## a1 1.9860307 0.03058033 1.9368689 2.034631 14116.13 1.0004122
## k 0.9721054 0.02159773 0.9382407 1.006761 15044.78 0.9995902
## tau 2.1898100 0.04953736 2.1120600 2.269831 14995.33 0.9999084post2 <- extract.samples(flbi_2, n = 10000)
quantile(post2$bx, probs = c(0.025, 0.5, 0.975))## 2.5% 50% 97.5%
## 7.061389 7.194525 7.327361Pensamientos finales
Parece que no es tan mala idea incluir en tu modelo bayesiano toda la información disponible.
Ser pluralista es una buena idea, usando el backdoor criterio dado que nuestro dag sea correcto, nos puede llevar a un modelo más simple y fácil de estimar.
Como dije en el último post, estimar todo el dag de forma conjunta puede ser útil en varias situaciones.
Ya en 2009 se hablaba de esto aquí