Recuerdo siendo yo más bisoño cuando escuché a los marketinianos hablar del A/B testing para acá , A/B testing para allá. En mi ingenuidad pensaba que era alguna clase de rito que sólo ellos conocían, y encima lo veía como requisito en las ofertas de empleo que miraba.
Mi decepción fue mayúscula cuando me enteré que esto del A/B testing no es más que un nombre marketiniano para hacer un contraste de proporciones o contrastes de medias, vamos, un prop.test o un t.test, ya que ni siquera trataban el caso de tener varios grupos o la existencia de covariables. Ains, esas dos asignaturas en la carrera de diseño de experimentos y de ver fórmulas y sumas de cuadrados a diestro y siniestro, esos anovas, y ancovas.
Total que hoy vengo a contar alguna forma diferente a la de la fórmula para hacer este tipo de contrastes.
Supongamos que tenemos los siguientes datos, inventados
df <- data.frame(
exitos = c(2, 200, 10, 20, 4, 200, 300, 20, 90, 90),
fracasos = c(8, 1000, 35, 80, 20, 400, 900, 400, 230, 150) ,
gcontrol = factor(c(1,0,1,1,1,0,0,0,0,0)))
df$n = df$exitos + df$fracasos
df## exitos fracasos gcontrol n
## 1 2 8 1 10
## 2 200 1000 0 1200
## 3 10 35 1 45
## 4 20 80 1 100
## 5 4 20 1 24
## 6 200 400 0 600
## 7 300 900 0 1200
## 8 20 400 0 420
## 9 90 230 0 320
## 10 90 150 0 240df$n = df$exitos + df$fracasosTenemos 10 experimentos binomiales y hemos obtenido esos resultados, (podría ser por ejemplo la proporción de clientes que han contratado un producto A en 10 meses)
Podriamos ver la proporción en cada fila
library(tidyverse)
df$prop <- df$exitos/df$n
df## exitos fracasos gcontrol n prop
## 1 2 8 1 10 0.20000000
## 2 200 1000 0 1200 0.16666667
## 3 10 35 1 45 0.22222222
## 4 20 80 1 100 0.20000000
## 5 4 20 1 24 0.16666667
## 6 200 400 0 600 0.33333333
## 7 300 900 0 1200 0.25000000
## 8 20 400 0 420 0.04761905
## 9 90 230 0 320 0.28125000
## 10 90 150 0 240 0.37500000ggplot(df, aes(prop, fill = gcontrol)) +
geom_density(alpha = 0.3) +
labs(fill = "Gcontrol")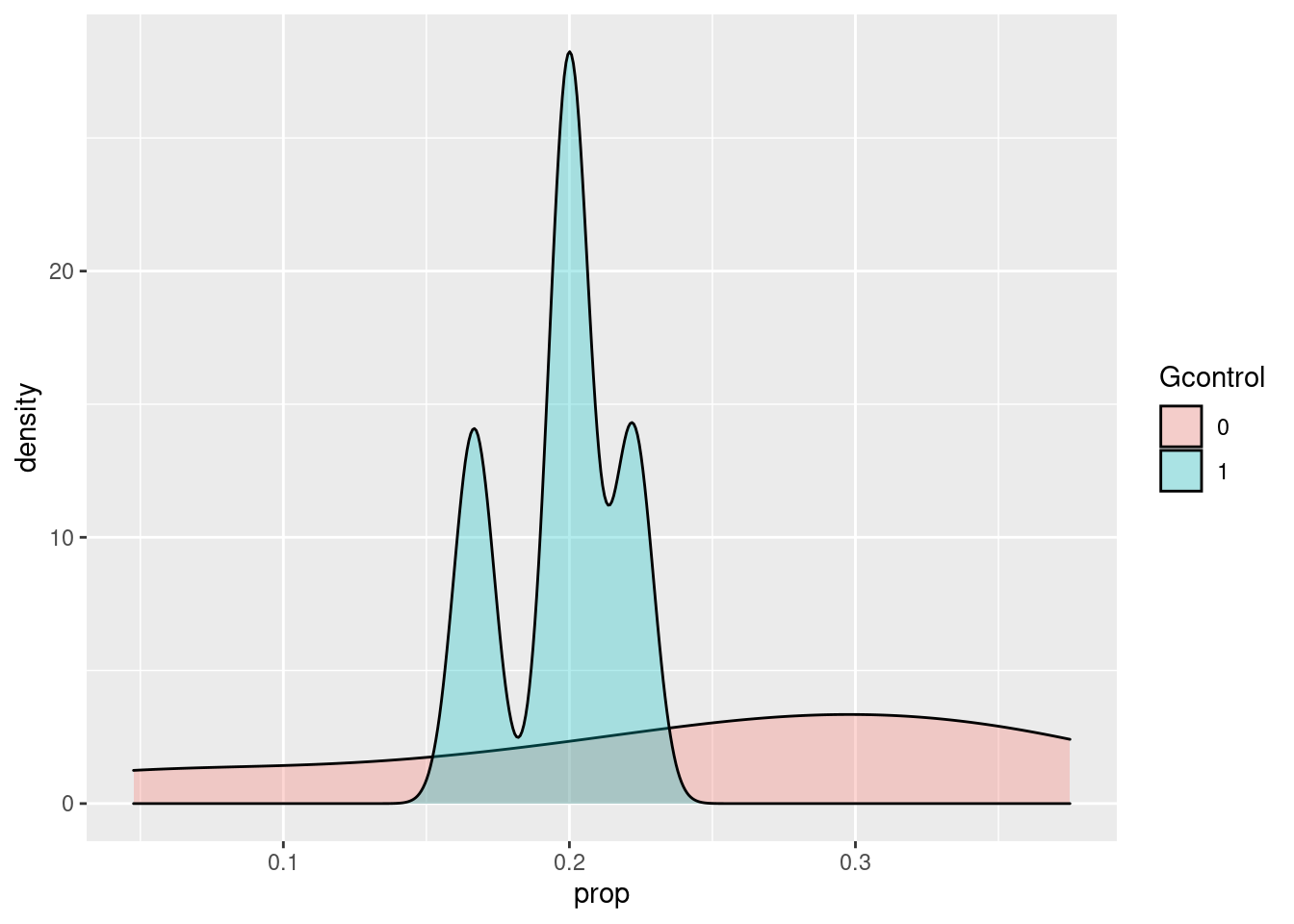
Pues como ahora me estoy volviendo bayesiano, ¿por qué no ajustar un modelo bayesiano a estos datos y obtener la posteriori de cada uno de las proporciones y de su diferencia. Vamos a ajustar lo que a veces se denomina una regresión binomial, dónde tenemos éxitos y ensayos. Normalmente la gente está acostumbrada a ajustar regresiones logísticas dónde la variable dependiente es 1 o 0, en este caso, la información está agregada, pero es equivalente.
Al tener el número de “ensayos” de cada experimento, se va a tener en cuenta, de forma que no va a ser lo mismo un experimento con 20 ensayos que uno con 200, aun cuando tengan la misma proporción.
Usando la librería brms y stan sería así de sencillo
library(brms)
library(cmdstanr)
set_cmdstan_path("~/cmdstan/")
prior <- get_prior(exitos | trials(n) ~ 0 + gcontrol ,
data = df,
family = binomial)
mod_brm <-
brm(data = df, family = binomial,
exitos | trials(n) ~ 0 + gcontrol,
prior = prior,
iter = 2500, warmup = 500, cores = 6, chains = 6,
seed = 10,
backend = "cmdstanr")## Running MCMC with 6 parallel chains...
##
## Chain 1 Iteration: 1 / 2500 [ 0%] (Warmup)
## Chain 1 Iteration: 100 / 2500 [ 4%] (Warmup)
## Chain 1 Iteration: 200 / 2500 [ 8%] (Warmup)
## Chain 1 Iteration: 300 / 2500 [ 12%] (Warmup)
## Chain 1 Iteration: 400 / 2500 [ 16%] (Warmup)
## Chain 1 Iteration: 500 / 2500 [ 20%] (Warmup)
## Chain 1 Iteration: 501 / 2500 [ 20%] (Sampling)
## Chain 1 Iteration: 600 / 2500 [ 24%] (Sampling)
## Chain 1 Iteration: 700 / 2500 [ 28%] (Sampling)
## Chain 1 Iteration: 800 / 2500 [ 32%] (Sampling)
## Chain 1 Iteration: 900 / 2500 [ 36%] (Sampling)
## Chain 1 Iteration: 1000 / 2500 [ 40%] (Sampling)
## Chain 1 Iteration: 1100 / 2500 [ 44%] (Sampling)
## Chain 1 Iteration: 1200 / 2500 [ 48%] (Sampling)
## Chain 1 Iteration: 1300 / 2500 [ 52%] (Sampling)
## Chain 1 Iteration: 1400 / 2500 [ 56%] (Sampling)
## Chain 1 Iteration: 1500 / 2500 [ 60%] (Sampling)
## Chain 1 Iteration: 1600 / 2500 [ 64%] (Sampling)
## Chain 1 Iteration: 1700 / 2500 [ 68%] (Sampling)
## Chain 1 Iteration: 1800 / 2500 [ 72%] (Sampling)
## Chain 1 Iteration: 1900 / 2500 [ 76%] (Sampling)
## Chain 1 Iteration: 2000 / 2500 [ 80%] (Sampling)
## Chain 1 Iteration: 2100 / 2500 [ 84%] (Sampling)
## Chain 1 Iteration: 2200 / 2500 [ 88%] (Sampling)
## Chain 1 Iteration: 2300 / 2500 [ 92%] (Sampling)
## Chain 1 Iteration: 2400 / 2500 [ 96%] (Sampling)
## Chain 1 Iteration: 2500 / 2500 [100%] (Sampling)
## Chain 2 Iteration: 1 / 2500 [ 0%] (Warmup)
## Chain 2 Iteration: 100 / 2500 [ 4%] (Warmup)
## Chain 2 Iteration: 200 / 2500 [ 8%] (Warmup)
## Chain 2 Iteration: 300 / 2500 [ 12%] (Warmup)
## Chain 2 Iteration: 400 / 2500 [ 16%] (Warmup)
## Chain 2 Iteration: 500 / 2500 [ 20%] (Warmup)
## Chain 2 Iteration: 501 / 2500 [ 20%] (Sampling)
## Chain 2 Iteration: 600 / 2500 [ 24%] (Sampling)
## Chain 2 Iteration: 700 / 2500 [ 28%] (Sampling)
## Chain 2 Iteration: 800 / 2500 [ 32%] (Sampling)
## Chain 2 Iteration: 900 / 2500 [ 36%] (Sampling)
## Chain 2 Iteration: 1000 / 2500 [ 40%] (Sampling)
## Chain 2 Iteration: 1100 / 2500 [ 44%] (Sampling)
## Chain 2 Iteration: 1200 / 2500 [ 48%] (Sampling)
## Chain 2 Iteration: 1300 / 2500 [ 52%] (Sampling)
## Chain 2 Iteration: 1400 / 2500 [ 56%] (Sampling)
## Chain 2 Iteration: 1500 / 2500 [ 60%] (Sampling)
## Chain 2 Iteration: 1600 / 2500 [ 64%] (Sampling)
## Chain 2 Iteration: 1700 / 2500 [ 68%] (Sampling)
## Chain 2 Iteration: 1800 / 2500 [ 72%] (Sampling)
## Chain 2 Iteration: 1900 / 2500 [ 76%] (Sampling)
## Chain 2 Iteration: 2000 / 2500 [ 80%] (Sampling)
## Chain 2 Iteration: 2100 / 2500 [ 84%] (Sampling)
## Chain 2 Iteration: 2200 / 2500 [ 88%] (Sampling)
## Chain 2 Iteration: 2300 / 2500 [ 92%] (Sampling)
## Chain 2 Iteration: 2400 / 2500 [ 96%] (Sampling)
## Chain 2 Iteration: 2500 / 2500 [100%] (Sampling)
## Chain 3 Iteration: 1 / 2500 [ 0%] (Warmup)
## Chain 3 Iteration: 100 / 2500 [ 4%] (Warmup)
## Chain 3 Iteration: 200 / 2500 [ 8%] (Warmup)
## Chain 3 Iteration: 300 / 2500 [ 12%] (Warmup)
## Chain 3 Iteration: 400 / 2500 [ 16%] (Warmup)
## Chain 3 Iteration: 500 / 2500 [ 20%] (Warmup)
## Chain 3 Iteration: 501 / 2500 [ 20%] (Sampling)
## Chain 3 Iteration: 600 / 2500 [ 24%] (Sampling)
## Chain 3 Iteration: 700 / 2500 [ 28%] (Sampling)
## Chain 3 Iteration: 800 / 2500 [ 32%] (Sampling)
## Chain 3 Iteration: 900 / 2500 [ 36%] (Sampling)
## Chain 3 Iteration: 1000 / 2500 [ 40%] (Sampling)
## Chain 3 Iteration: 1100 / 2500 [ 44%] (Sampling)
## Chain 3 Iteration: 1200 / 2500 [ 48%] (Sampling)
## Chain 3 Iteration: 1300 / 2500 [ 52%] (Sampling)
## Chain 3 Iteration: 1400 / 2500 [ 56%] (Sampling)
## Chain 3 Iteration: 1500 / 2500 [ 60%] (Sampling)
## Chain 3 Iteration: 1600 / 2500 [ 64%] (Sampling)
## Chain 3 Iteration: 1700 / 2500 [ 68%] (Sampling)
## Chain 3 Iteration: 1800 / 2500 [ 72%] (Sampling)
## Chain 3 Iteration: 1900 / 2500 [ 76%] (Sampling)
## Chain 3 Iteration: 2000 / 2500 [ 80%] (Sampling)
## Chain 3 Iteration: 2100 / 2500 [ 84%] (Sampling)
## Chain 3 Iteration: 2200 / 2500 [ 88%] (Sampling)
## Chain 3 Iteration: 2300 / 2500 [ 92%] (Sampling)
## Chain 3 Iteration: 2400 / 2500 [ 96%] (Sampling)
## Chain 3 Iteration: 2500 / 2500 [100%] (Sampling)
## Chain 4 Iteration: 1 / 2500 [ 0%] (Warmup)
## Chain 4 Iteration: 100 / 2500 [ 4%] (Warmup)
## Chain 4 Iteration: 200 / 2500 [ 8%] (Warmup)
## Chain 4 Iteration: 300 / 2500 [ 12%] (Warmup)
## Chain 4 Iteration: 400 / 2500 [ 16%] (Warmup)
## Chain 4 Iteration: 500 / 2500 [ 20%] (Warmup)
## Chain 4 Iteration: 501 / 2500 [ 20%] (Sampling)
## Chain 4 Iteration: 600 / 2500 [ 24%] (Sampling)
## Chain 4 Iteration: 700 / 2500 [ 28%] (Sampling)
## Chain 4 Iteration: 800 / 2500 [ 32%] (Sampling)
## Chain 4 Iteration: 900 / 2500 [ 36%] (Sampling)
## Chain 4 Iteration: 1000 / 2500 [ 40%] (Sampling)
## Chain 4 Iteration: 1100 / 2500 [ 44%] (Sampling)
## Chain 4 Iteration: 1200 / 2500 [ 48%] (Sampling)
## Chain 4 Iteration: 1300 / 2500 [ 52%] (Sampling)
## Chain 4 Iteration: 1400 / 2500 [ 56%] (Sampling)
## Chain 4 Iteration: 1500 / 2500 [ 60%] (Sampling)
## Chain 4 Iteration: 1600 / 2500 [ 64%] (Sampling)
## Chain 4 Iteration: 1700 / 2500 [ 68%] (Sampling)
## Chain 4 Iteration: 1800 / 2500 [ 72%] (Sampling)
## Chain 4 Iteration: 1900 / 2500 [ 76%] (Sampling)
## Chain 4 Iteration: 2000 / 2500 [ 80%] (Sampling)
## Chain 4 Iteration: 2100 / 2500 [ 84%] (Sampling)
## Chain 4 Iteration: 2200 / 2500 [ 88%] (Sampling)
## Chain 4 Iteration: 2300 / 2500 [ 92%] (Sampling)
## Chain 4 Iteration: 2400 / 2500 [ 96%] (Sampling)
## Chain 4 Iteration: 2500 / 2500 [100%] (Sampling)
## Chain 5 Iteration: 1 / 2500 [ 0%] (Warmup)
## Chain 5 Iteration: 100 / 2500 [ 4%] (Warmup)
## Chain 5 Iteration: 200 / 2500 [ 8%] (Warmup)
## Chain 5 Iteration: 300 / 2500 [ 12%] (Warmup)
## Chain 5 Iteration: 400 / 2500 [ 16%] (Warmup)
## Chain 5 Iteration: 500 / 2500 [ 20%] (Warmup)
## Chain 5 Iteration: 501 / 2500 [ 20%] (Sampling)
## Chain 5 Iteration: 600 / 2500 [ 24%] (Sampling)
## Chain 5 Iteration: 700 / 2500 [ 28%] (Sampling)
## Chain 5 Iteration: 800 / 2500 [ 32%] (Sampling)
## Chain 5 Iteration: 900 / 2500 [ 36%] (Sampling)
## Chain 5 Iteration: 1000 / 2500 [ 40%] (Sampling)
## Chain 5 Iteration: 1100 / 2500 [ 44%] (Sampling)
## Chain 5 Iteration: 1200 / 2500 [ 48%] (Sampling)
## Chain 5 Iteration: 1300 / 2500 [ 52%] (Sampling)
## Chain 5 Iteration: 1400 / 2500 [ 56%] (Sampling)
## Chain 5 Iteration: 1500 / 2500 [ 60%] (Sampling)
## Chain 5 Iteration: 1600 / 2500 [ 64%] (Sampling)
## Chain 5 Iteration: 1700 / 2500 [ 68%] (Sampling)
## Chain 5 Iteration: 1800 / 2500 [ 72%] (Sampling)
## Chain 5 Iteration: 1900 / 2500 [ 76%] (Sampling)
## Chain 5 Iteration: 2000 / 2500 [ 80%] (Sampling)
## Chain 5 Iteration: 2100 / 2500 [ 84%] (Sampling)
## Chain 5 Iteration: 2200 / 2500 [ 88%] (Sampling)
## Chain 5 Iteration: 2300 / 2500 [ 92%] (Sampling)
## Chain 5 Iteration: 2400 / 2500 [ 96%] (Sampling)
## Chain 5 Iteration: 2500 / 2500 [100%] (Sampling)
## Chain 6 Iteration: 1 / 2500 [ 0%] (Warmup)
## Chain 6 Iteration: 100 / 2500 [ 4%] (Warmup)
## Chain 6 Iteration: 200 / 2500 [ 8%] (Warmup)
## Chain 6 Iteration: 300 / 2500 [ 12%] (Warmup)
## Chain 6 Iteration: 400 / 2500 [ 16%] (Warmup)
## Chain 6 Iteration: 500 / 2500 [ 20%] (Warmup)
## Chain 6 Iteration: 501 / 2500 [ 20%] (Sampling)
## Chain 6 Iteration: 600 / 2500 [ 24%] (Sampling)
## Chain 6 Iteration: 700 / 2500 [ 28%] (Sampling)
## Chain 6 Iteration: 800 / 2500 [ 32%] (Sampling)
## Chain 6 Iteration: 900 / 2500 [ 36%] (Sampling)
## Chain 6 Iteration: 1000 / 2500 [ 40%] (Sampling)
## Chain 6 Iteration: 1100 / 2500 [ 44%] (Sampling)
## Chain 6 Iteration: 1200 / 2500 [ 48%] (Sampling)
## Chain 6 Iteration: 1300 / 2500 [ 52%] (Sampling)
## Chain 6 Iteration: 1400 / 2500 [ 56%] (Sampling)
## Chain 6 Iteration: 1500 / 2500 [ 60%] (Sampling)
## Chain 6 Iteration: 1600 / 2500 [ 64%] (Sampling)
## Chain 6 Iteration: 1700 / 2500 [ 68%] (Sampling)
## Chain 6 Iteration: 1800 / 2500 [ 72%] (Sampling)
## Chain 6 Iteration: 1900 / 2500 [ 76%] (Sampling)
## Chain 6 Iteration: 2000 / 2500 [ 80%] (Sampling)
## Chain 6 Iteration: 2100 / 2500 [ 84%] (Sampling)
## Chain 6 Iteration: 2200 / 2500 [ 88%] (Sampling)
## Chain 6 Iteration: 2300 / 2500 [ 92%] (Sampling)
## Chain 6 Iteration: 2400 / 2500 [ 96%] (Sampling)
## Chain 6 Iteration: 2500 / 2500 [100%] (Sampling)
## Chain 1 finished in 0.1 seconds.
## Chain 2 finished in 0.1 seconds.
## Chain 3 finished in 0.1 seconds.
## Chain 4 finished in 0.1 seconds.
## Chain 5 finished in 0.1 seconds.
## Chain 6 finished in 0.1 seconds.
##
## All 6 chains finished successfully.
## Mean chain execution time: 0.1 seconds.
## Total execution time: 0.6 seconds.fixef(mod_brm) %>%
round(digits = 2)## Estimate Est.Error Q2.5 Q97.5
## gcontrol0 -1.23 0.04 -1.31 -1.16
## gcontrol1 -1.39 0.19 -1.77 -1.03Y ya tengo la estimación de cada proporción sin más que hacer el invlogit
fixef(mod_brm) %>%
round(digits = 2) %>%
inv_logit_scaled()## Estimate Est.Error Q2.5 Q97.5
## gcontrol0 0.2261814 0.5099987 0.2124868 0.2386673
## gcontrol1 0.1994078 0.5473576 0.1455423 0.2630841Una cosa buena de la estimación bayesiana es que tengo la posteriori completa de ambas proporciones
post <- as_tibble(mod_brm)
post## # A tibble: 12,000 × 3
## b_gcontrol0 b_gcontrol1 lp__
## <dbl> <dbl> <dbl>
## 1 -1.17 -1.39 -128.
## 2 -1.18 -1.38 -128.
## 3 -1.20 -1.10 -128.
## 4 -1.24 -1.45 -127.
## 5 -1.23 -1.79 -129.
## 6 -1.21 -1.60 -128.
## 7 -1.21 -1.62 -128.
## 8 -1.19 -1.68 -129.
## 9 -1.19 -1.59 -128.
## 10 -1.30 -1.54 -129.
## # … with 11,990 more rowsY tenemos 2000 muestras por 6 cadenas, 12000 muestras aleatorias de cada proporción.
Ahora puedo hacer cosas como ver la distribución a posteriori de la diferencia
post$diferencia = inv_logit_scaled(post$b_gcontrol1) - inv_logit_scaled(post$b_gcontrol0)
ggplot(post, aes(diferencia)) +
geom_density()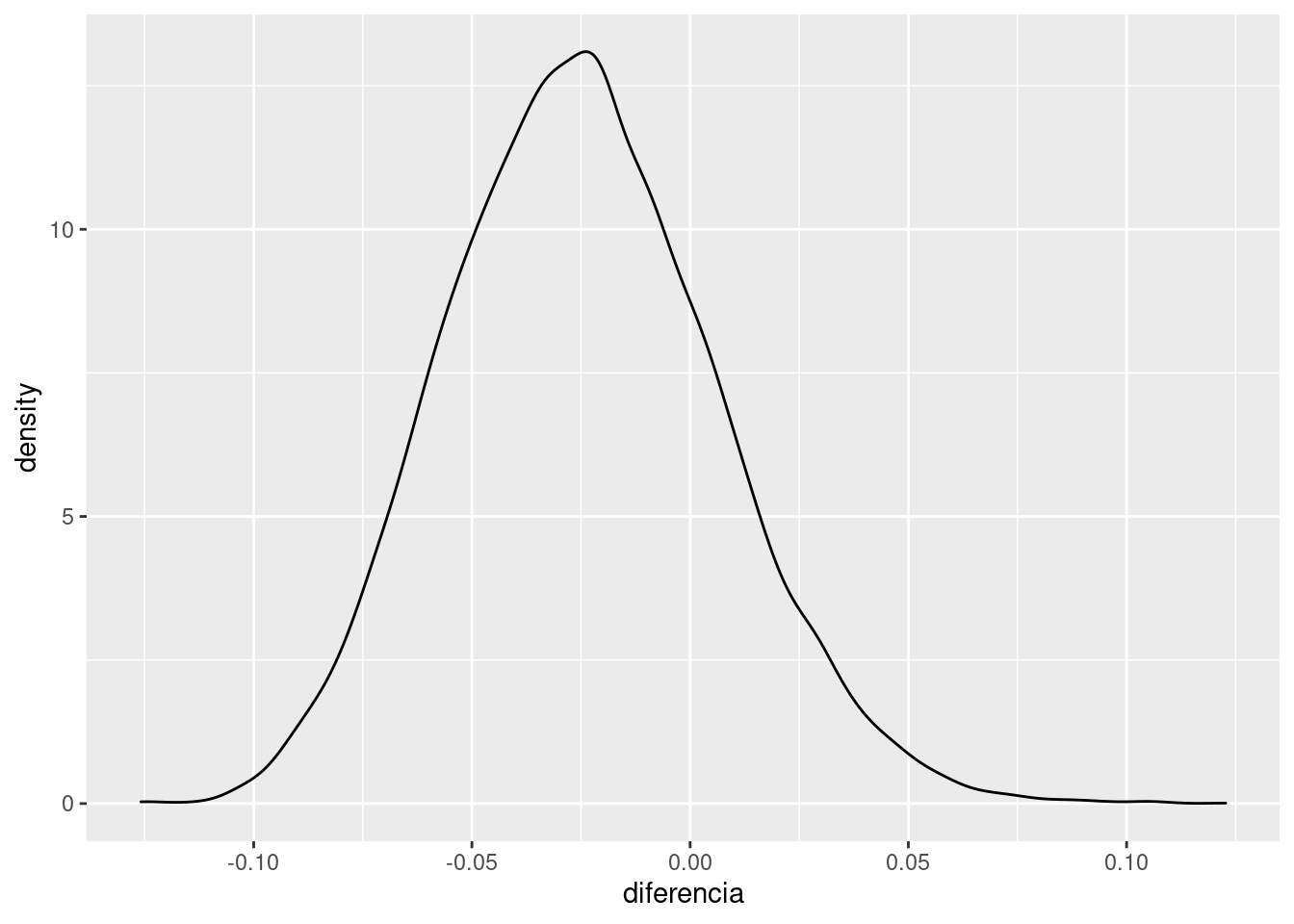
Intervalo de credibilidad al 80%
quantile(post$diferencia, probs = c(0.1,0.9))## 10% 90%
## -0.06377131 0.01499445Y si sospechamos que hay más estructura en nuestros datos podemos modelarla igulmente, por ejemplo las proporciones podrían tener relación con el mes del año o con cualquier otra cosa.
En fin, un método alternativo para hacer A/B testing o como se llame ahora.
comments powered by Disqus