A pesar del título, no voy a hablar sobre la excelente canción de los Suaves, sino del lenguaje de programación Julia. Ya en otra entrada del blog de hace un par de años comparé glmer con INLA y la librería MixedModels. Por aquel entonces la versión de Julia era la 1.0.3, ya va por la 1.6.2. Debido a reciente entrada de Carlos dónde apostaba por Julia para el larguísimo plazo, he decidido echarle un vistazo un poco más en profundidad.
Lo cierto es que me está gustando bastante el lenguaje y voy a escribir un par de entradas dónde contar alguna cosilla. Ya Carlos mencionaba que Julia corre sobre LLVM, pero también cabe mencionar que Julia tiene características más que interesantes, como multiple dispatch o tipos abstractos que permiten al desarrollador escribir código sin preocuparse demasiado por el tipado y que sea el compilador el que cree los métodos específicos. Si, has oído bien, Julia compila las funciones, por lo que tiene la doble ventaja de ser un lenguaje rápido a la vez que sencillo, bueno, su lema dice “Tan fácil como Python, tan rápido como C”.
En esta primera entrada voy a poner un ejemplo sencillo de cómo sería hacer un modelo de “Machín Lenin” utilizando la librería MLJ, y en el post siguiente os contaré como tener un binario para predecir usando ese modelo de forma que funcione en cualquier Linux sin importar si está basado en Debian, Centos o lo que sea, y sin necesidad de tener instalado Julia, ni docker, ni nada.
Modelo con MLJ
MLJ es una librería que pretende servir de interfaz común a otras muchas librerías. Veamos un ejemplo de como ajustar un RandomForest implementado en la librería DecisionTree.
Lo primero, para instalar paquetes podéis mirar esto, básicamente haces
using Pkg
Pkg.import("nombre_paquete")
O en el REPL de Julia entras en el modo Package pulsando ] y pones add nombre_paquete . Esto bajará la librería correspondiente precompilado y la añade a ~/.julia/packages/
Vamos al ejemplo. Aunque voy a usar chunks de julia (gracias a la librería JuliaCall) en el rmarkdown dónde escribo los posts, en realidad como editor par Julia me gusta VSCode.
Los datos de ejemplo son de la librería bootde R . puedes ver la ayuda haciendo en R
library(boot)
help(channing)Channing House Data
Description
The channing data frame has 462 rows and 5 columns.
Channing House is a retirement centre in Palo Alto, California. These data were collected between the opening of the house in 1964 until July 1, 1975. In that time 97 men and 365 women passed through the centre. For each of these, their age on entry and also on leaving or death was recorded. A large number of the observations were censored mainly due to the resident being alive on July 1, 1975 when the data was collected. Over the time of the study 130 women and 46 men died at Channing House. Differences between the survival of the sexes, taking age into account, was one of the primary concerns of this study.
Usage
channing
Format
This data frame contains the following columns:
sex
A factor for the sex of each resident ("Male" or "Female").
entry
The residents age (in months) on entry to the centre
exit
The age (in months) of the resident on death, leaving the centre or July 1, 1975 whichever event occurred first.
time
The length of time (in months) that the resident spent at Channing House. (time=exit-entry)
cens
The indicator of right censoring. 1 indicates that the resident died at Channing House, 0 indicates that they left the house prior to July 1, 1975 or that they were still alive and living in the centre at that date.
En Julia podemos instalar la librería RDatasets y usar esos datos
using RDatasets, MLJ
channing = dataset("boot", "channing")## 462×5 DataFrame
## Row │ Sex Entry Exit Time Cens
## │ Cat… Int32 Int32 Int32 Int32
## ─────┼────────────────────────────────────
## 1 │ Male 782 909 127 1
## 2 │ Male 1020 1128 108 1
## 3 │ Male 856 969 113 1
## 4 │ Male 915 957 42 1
## 5 │ Male 863 983 120 1
## 6 │ Male 906 1012 106 1
## 7 │ Male 955 1055 100 1
## 8 │ Male 943 1025 82 1
## ⋮ │ ⋮ ⋮ ⋮ ⋮ ⋮
## 456 │ Female 986 1030 44 1
## 457 │ Female 1039 1132 93 1
## 458 │ Female 968 990 22 1
## 459 │ Female 955 990 35 1
## 460 │ Female 837 911 74 1
## 461 │ Female 861 915 54 1
## 462 │ Female 967 983 16 1
## 447 rows omittedMLJ necesita que las columnas tenga los tipos correctos en scitypes. Podemos verlos con
schema(channing)## ┌─────────┬─────────────────────────────────┬───────────────┐
## │ _.names │ _.types │ _.scitypes │
## ├─────────┼─────────────────────────────────┼───────────────┤
## │ Sex │ CategoricalValue{String, UInt8} │ Multiclass{2} │
## │ Entry │ Int32 │ Count │
## │ Exit │ Int32 │ Count │
## │ Time │ Int32 │ Count │
## │ Cens │ Int32 │ Count │
## └─────────┴─────────────────────────────────┴───────────────┘
## _.nrows = 462Queremos modelar la variable exit. MLJ quiere la y por un lado y las X’s por otro, para eso vamos a usar la función unpack que además de permitir eso permite cambiar el tipo de las variables, y convertir la variable Cens a categórica por ejemplo
y, X = unpack(channing,
==(:Exit), # con el doble igual seleccionamos la y
!=(:Time); # Quitamos variable Time
:Exit=>Continuous, # Convertimos al tipo correcto en scitypes
:Entry=>Continuous,
:Cens=>Multiclass)## ([909.0, 1128.0, 969.0, 957.0, 983.0, 1012.0, 1055.0, 1025.0, 1043.0, 945.0 … 905.0, 1040.0, 926.0, 1030.0, 1132.0, 990.0, 990.0, 911.0, 915.0, 983.0], 462×3 DataFrame
## Row │ Sex Entry Cens
## │ Cat… Float64 Cat…
## ─────┼───────────────────────
## 1 │ Male 782.0 1
## 2 │ Male 1020.0 1
## 3 │ Male 856.0 1
## 4 │ Male 915.0 1
## 5 │ Male 863.0 1
## 6 │ Male 906.0 1
## 7 │ Male 955.0 1
## 8 │ Male 943.0 1
## ⋮ │ ⋮ ⋮ ⋮
## 456 │ Female 986.0 1
## 457 │ Female 1039.0 1
## 458 │ Female 968.0 1
## 459 │ Female 955.0 1
## 460 │ Female 837.0 1
## 461 │ Female 861.0 1
## 462 │ Female 967.0 1
## 447 rows omitted)Ahora ya podemos ver como se hace el modelo.
Tree = @load RandomForestRegressor pkg=DecisionTree## import MLJDecisionTreeInterface ✔## MLJDecisionTreeInterface.RandomForestRegressortree = Tree(n_trees = 20) # tambien se puede instanciar sin paraámetros ## RandomForestRegressor(
## max_depth = -1,
## min_samples_leaf = 1,
## min_samples_split = 2,
## min_purity_increase = 0.0,
## n_subfeatures = -1,
## n_trees = 20,
## sampling_fraction = 0.7,
## pdf_smoothing = 0.0)[34m @867[39m# y usar tree.n_trees = 20
Como tenemos la variable Censque es categórica necesitamos codificarla, aquí entra como hacer un pipeline en MLJ, que es una de las cosas más potentes que tiene junto con los ComposingModels models que permite mezclar varios modelos.
# Definimos un ContinuosEncoder, ver la ayuda con ?ContinousEncoder en el repl de julia
ContinuousEncoder(one_hot_ordered_factors=false, drop_last=false)## ContinuousEncoder(
## drop_last = false,
## one_hot_ordered_factors = false)[34m @541[39m
# Unsupervised model for arranging all features (columns) of a table to have Continuous element scitype, by applying the following protocol to each feature ftr:
#
# • If ftr is already Continuous retain it.
#
# • If ftr is Multiclass, one-hot encode it.
#
# • If ftr is OrderedFactor, replace it with coerce(ftr, Continuous) (vector of floating point integers), unless ordered_factors=false is specified, in which case
# one-hot encode it.
#
# • If ftr is Count, replace it with coerce(ftr, Continuous).
#
# • If ftr is of some other element scitype, or was not observed in fitting the encoder, drop it from the table.
#
# If drop_last=true is specified, then one-hot encoding always drops the last class indicator colum
hot = ContinuousEncoder(one_hot_ordered_factors=true, drop_last=true)## ContinuousEncoder(
## drop_last = true,
## one_hot_ordered_factors = true)[34m @184[39mUtilizamos la macro @pipeline para encadenar el onehot y el modelo
pipe = @pipeline hot tree## Pipeline259(
## continuous_encoder = ContinuousEncoder(
## drop_last = true,
## one_hot_ordered_factors = true),
## random_forest_regressor = RandomForestRegressor(
## max_depth = -1,
## min_samples_leaf = 1,
## min_samples_split = 2,
## min_purity_increase = 0.0,
## n_subfeatures = -1,
## n_trees = 20,
## sampling_fraction = 0.7,
## pdf_smoothing = 0.0))[34m @513[39mY ya podemos ajustar el modelo por ejemplo utilizando evaluate y validación cruzada
evaluate(pipe, X, y, resampling=CV(nfolds=5), measure = [rmse, mae])## ┌───────────────────────────┬───────────────┬────────────────────────────────┐
## │ _.measure │ _.measurement │ _.per_fold │
## ├───────────────────────────┼───────────────┼────────────────────────────────┤
## │ RootMeanSquaredError @956 │ 55.6 │ [48.1, 62.0, 53.8, 50.5, 61.9] │
## │ MeanAbsoluteError @225 │ 46.6 │ [40.9, 53.1, 43.8, 42.0, 53.4] │
## └───────────────────────────┴───────────────┴────────────────────────────────┘
## _.per_observation = [missing, missing]
## _.fitted_params_per_fold = [ … ]
## _.report_per_fold = [ … ]Hay más medidas que se pueden listar con measures()
También podemos partir en train, test y similar
train, test = partition(eachindex(y), 0.7, shuffle=true, rng=155);Ahora instanciamos el modelo con machine especificando la X, y la y
modelo = machine(pipe, X,y)## [34mMachine{Pipeline259,…} @980[39m trained 0 times; caches data
## args:
## 1: [34mSource @265[39m ⏎ `Table{Union{AbstractVector{Continuous}, AbstractVector{Multiclass{2}}}}`
## 2: [34mSource @897[39m ⏎ `AbstractVector{Continuous}`Y podemos usar fit! para ajustar “in place” (en julia si la función acaba en ! es una función que actua modificando el objeto que se le pasa) sin tener que crear otra variable
fit!(modelo, rows = train)## [34mMachine{Pipeline259,…} @980[39m trained 1 time; caches data
## args:
## 1: [34mSource @265[39m ⏎ `Table{Union{AbstractVector{Continuous}, AbstractVector{Multiclass{2}}}}`
## 2: [34mSource @897[39m ⏎ `AbstractVector{Continuous}`Y ya podríamos predecir sobre test, dónde se le aplicaría el onehot encoder que hemos definido en el pipeline
# En julia podemos usar sintaxis latex por ejemplo \beta\hat y tabulador despues de beta y hat en vscode
# escribe β̂ (uso juliaMono https://juliamono.netlify.app/) como tipo de letra
ŷ = predict(modelo,X[test, :])## 139-element Vector{Float64}:
## 1068.7
## 1069.05
## 1025.6166666666666
## 1025.85
## 933.4083333333332
## 956.5
## 1119.25
## 968.6666666666666
## 949.1375
## 866.4625
## ⋮
## 883.2175
## 867.725
## 1021.2833333333332
## 936.0666666666668
## 938.7166666666668
## 929.85
## 1077.9333333333334
## 945.1625
## 944.9625En este caso hemos hecho un modelo para predecir una variable continua, cuando sea categórica existen funciones que devuelven la clase predicha o la probabilidad de cada clase.
También podemos ver como varía el error según el número de árboles
modelo## [34mMachine{Pipeline259,…} @980[39m trained 1 time; caches data
## args:
## 1: [34mSource @265[39m ⏎ `Table{Union{AbstractVector{Continuous}, AbstractVector{Multiclass{2}}}}`
## 2: [34mSource @897[39m ⏎ `AbstractVector{Continuous}`r_tree = range(pipe, :(random_forest_regressor.n_trees), lower=2, upper=20)## typename(MLJBase.NumericRange)(Int64, :(random_forest_regressor.n_trees), ... )
curve = MLJ.learning_curve(modelo;
range=r_tree,
resampling=CV(nfolds=5),
measure=rmse)## (parameter_name = "random_forest_regressor.n_trees",
## parameter_scale = :linear,
## parameter_values = [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20],
## measurements = [65.42183246458882, 59.11119640237987, 55.7512163366967, 58.34159065560261, 57.134134628248496, 56.97838965317687, 56.68078029656279, 56.19162995151205, 57.57519156288071, 55.922943397008744, 55.16193489943914, 55.83221711509146, 56.205393291313506, 56.830588361395094, 56.49114184998105, 55.58539209834001, 56.418841059687026, 56.17205183553797, 56.171363302332196],)using Plots
gr() # especificamos un ## Plots.GRBackend()plot(curve.parameter_values,
curve.measurements,
xlab=curve.parameter_name,
xscale=curve.parameter_scale,
ylab = "CV estimate of RMSE error")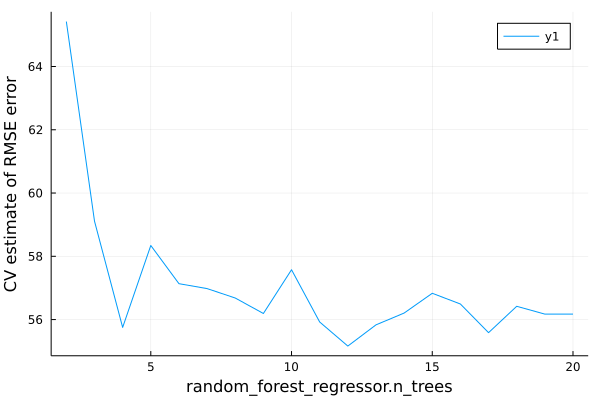
Y esto es todo, en el próximo post contaré como crear el binario que nos va a permitir tener un motor de predicción para los modelos de un árbol de decisión y que funcione en cualquier linux. Casi listo para producción (o al menos una parte importante) sin tener que tener julia en dónde se vaya a utilizar.