Bueno, pues voy a ampliar el ejemplo del último día, como es viernes, estoy cansado y me iré a tomar una birra pronto, intentaré ser breve.
Levantamos una sesión de spark y leemos los mismos datos del otro día. Ya de paso voy a probar el operador pipe nativo en R base |>. Si tienes la nueva versión de R instalada y la versión de Rstudio preview, en global options puedes poner para que al hacer Ctrl + Shift +M aparezca el nuevo operador o el antiguo.
library(tidyverse)
library(sparklyr)
sc <- spark_connect(master = "local")
tmp <- sc |>
spark_read_parquet(path = here::here("data/bd_pobres.parquet" ))# en el nuevo operador es necesario el paréntesis.
tmp |> head()## # Source: spark<?> [?? x 4]
## valor_cliente edad segmento tipo
## <dbl> <dbl> <chr> <chr>
## 1 3 79 No_way B
## 2 3 79 No_way B
## 3 3 79 No_way B
## 4 3 79 No_way B
## 5 3 79 No_way B
## 6 3 79 No_way BDiscretizamos la edad.
df_spark <- tmp |>
mutate(
edad_cat = case_when(
edad <= 20 ~ "<21",
edad <= 40 ~ "21- 40",
edad <= 50 ~ "41-50",
edad <= 60 ~ "40-60",
edad > 60 ~ ">60"
)
)
head(df_spark)## # Source: spark<?> [?? x 5]
## valor_cliente edad segmento tipo edad_cat
## <dbl> <dbl> <chr> <chr> <chr>
## 1 3 79 No_way B >60
## 2 3 79 No_way B >60
## 3 3 79 No_way B >60
## 4 3 79 No_way B >60
## 5 3 79 No_way B >60
## 6 3 79 No_way B >60Y ahora vamos a crear conjunto de train y de test
particiones <- df_spark |> sdf_random_split(training = 0.6, test = 0.4)
train <- particiones$training
test <- particiones$test Y ahora procedemos a agregar los datos y traerlos a local. Y seguro que alguno se pregunta ¿por qué no haces el modelo en spark?. Podría hacerlo, ya he contado en este blog como hacer modelos usando sparkling water por ejemplo, pero podría querer ajustar un tipo de modelo que no esté en distribuido, no sé, un modelo mixto con glmer o con stan . De hecho es eso lo que voy a hacer, un glmer.
train_local <- train |>
group_by(segmento,
tipo,
valor_cliente,
edad_cat) |>
count() |>
collect() |>
# ponemos las variables categóricas a tipo factor
mutate(across(where(is.character), as_factor))
DT::datatable(train_local)Tenemos 667 filas con la info de 1.456239^{6} observaciones
Agregamos y bajamos el test
test_local <- test |>
group_by(segmento,
tipo,
valor_cliente,
edad_cat) |>
count() |>
collect() |>
# ponemos las variables categóricas a tipo factor
mutate(across(where(is.character), as_factor))
DT::datatable(test_local)Tenemos 655 con la info de 9.72147^{5} observaciones
# desconectamos spark
spark_disconnect(sc)glmer
Hacemos un par de modelos mixtos como en el post anterior, pero en los datos de train
library(lme4)
modA <- glmer(segmento == "Best" ~ (1 | edad_cat) + (1 | valor_cliente) + (1 | tipo),
data = train_local, family= binomial, weights= train_local$n)
modB <- glmer(segmento == "No_way" ~(1 | edad_cat) + (1 |valor_cliente) + (1 | tipo),
data = train_local, family= binomial, weights= train_local$n) Podemos ver el modelo A por ejemplo
summary(modA)## Generalized linear mixed model fit by maximum likelihood (Laplace
## Approximation) [glmerMod]
## Family: binomial ( logit )
## Formula: segmento == "Best" ~ (1 | edad_cat) + (1 | valor_cliente) + (1 |
## tipo)
## Data: train_local
## Weights: train_local$n
##
## AIC BIC logLik deviance df.resid
## 794795.3 794813.3 -397393.6 794787.3 663
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -71.799 -6.459 -2.006 1.667 281.127
##
## Random effects:
## Groups Name Variance Std.Dev.
## valor_cliente (Intercept) 0.06432 0.2536
## edad_cat (Intercept) 0.39504 0.6285
## tipo (Intercept) 0.01669 0.1292
## Number of obs: 667, groups: valor_cliente, 10; edad_cat, 5; tipo, 4
##
## Fixed effects:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -2.0928 0.3023 -6.923 4.41e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1sjPlot::plot_model(modA, type = "re")## [[1]]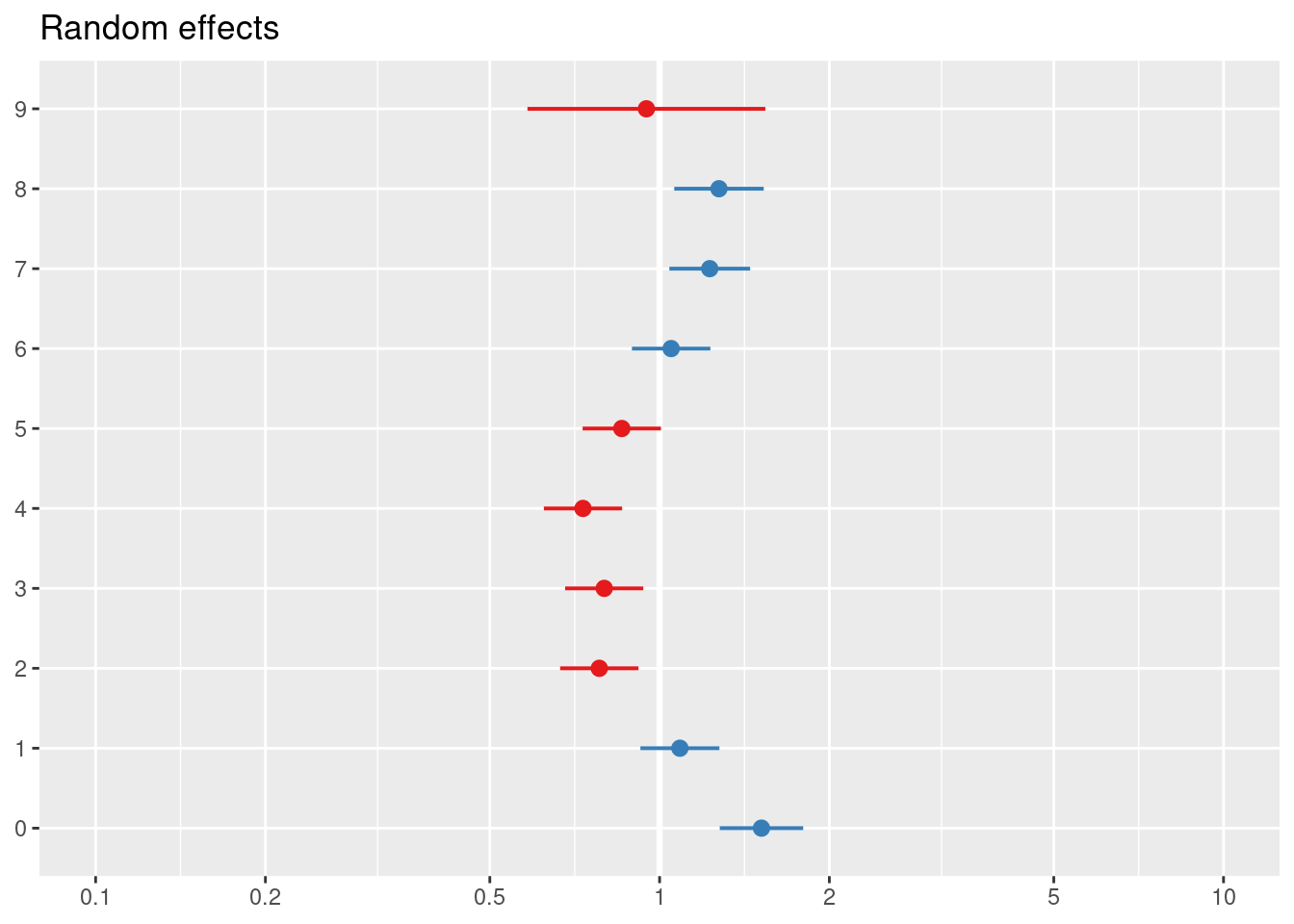
##
## [[2]]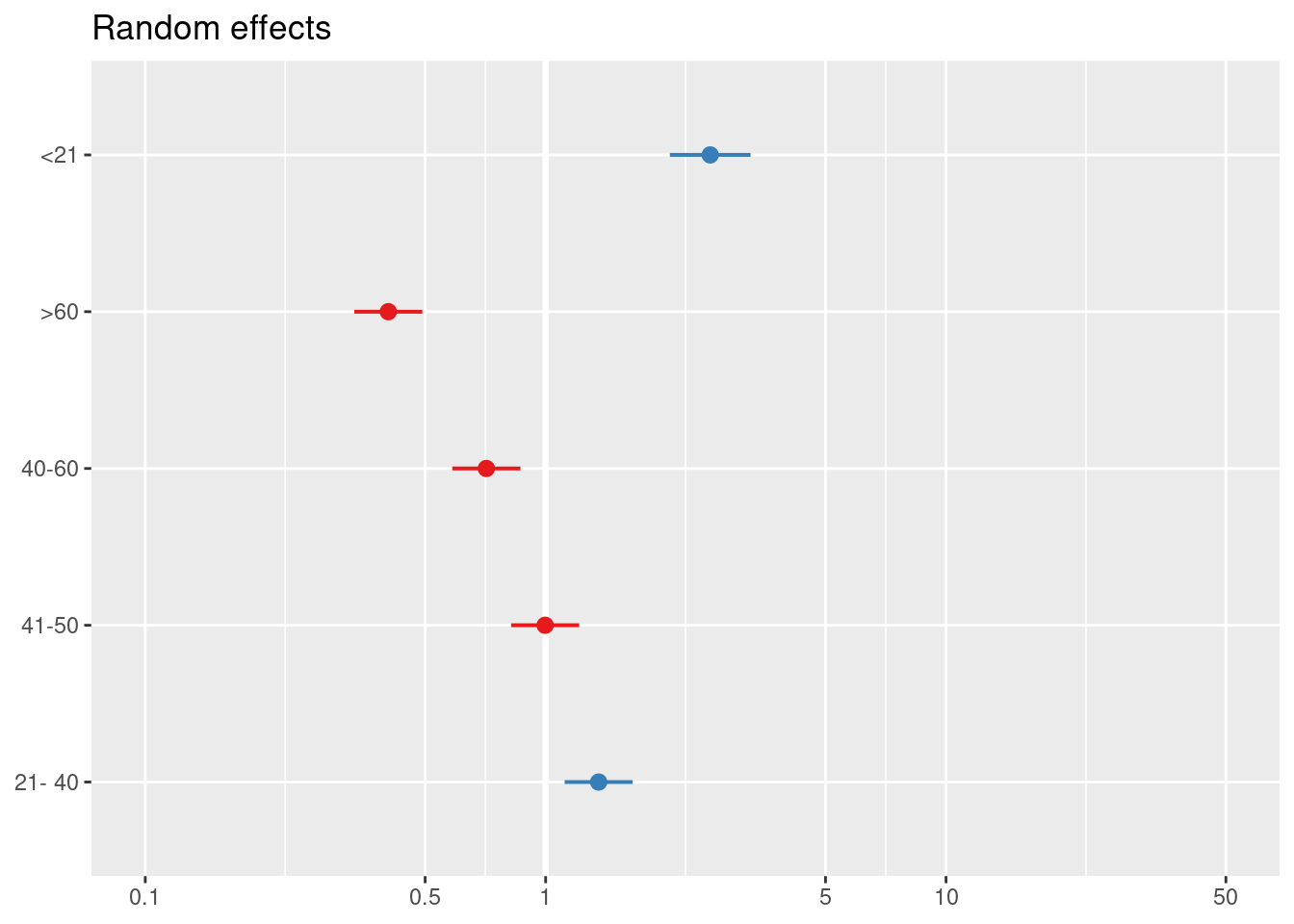
##
## [[3]]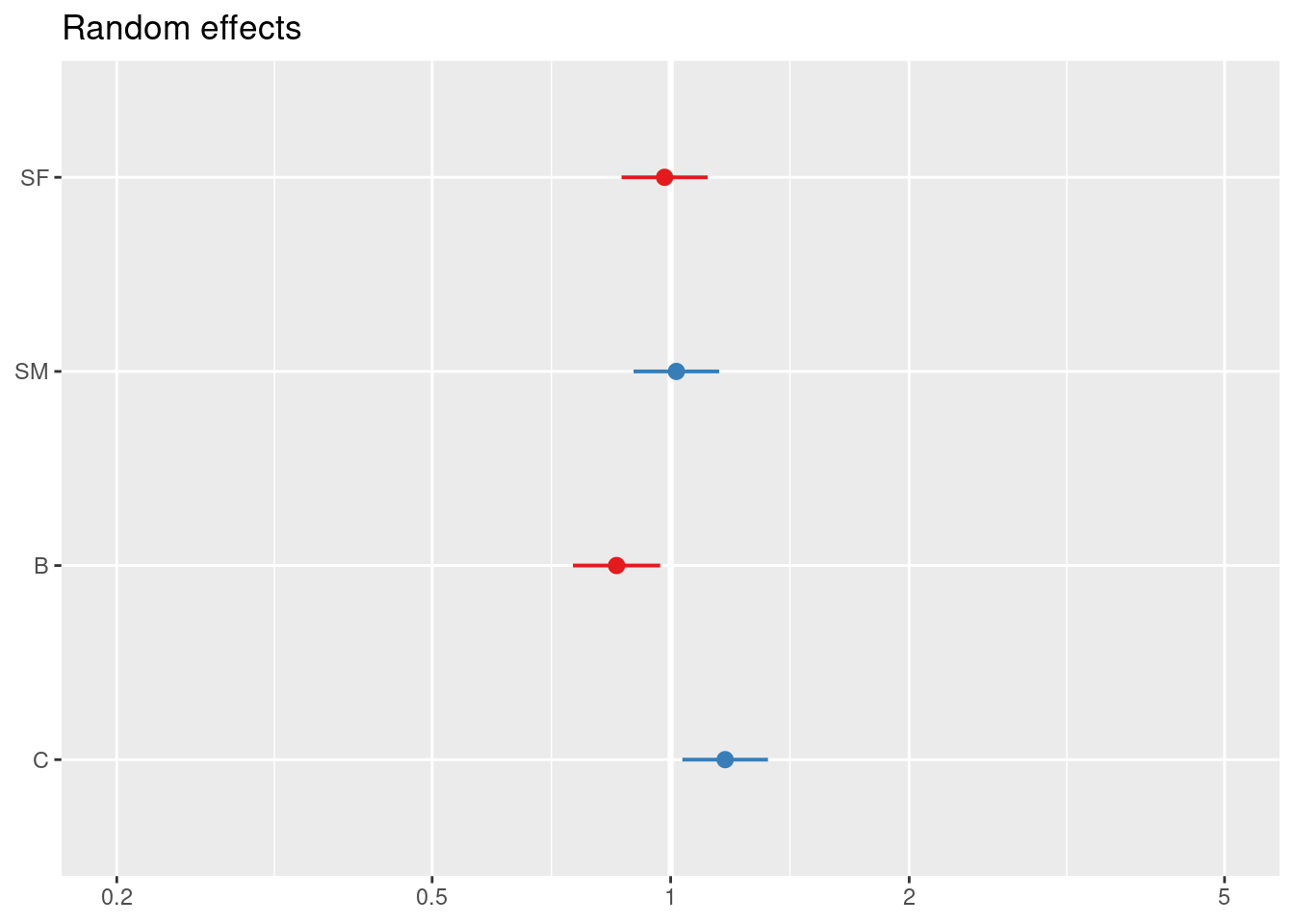
Predicción del glmer
Ahora hacemos predicción sobre el conjunto de test, que recordemos también está en formato de datos agregados.
test_local$Apredict <- predict(modA, newdata = test_local,
allow.new.levels= TRUE,
type= "response")
test_local$Bpredict <- predict(modB, newdata = test_local,
allow.new.levels= TRUE,
type= "response")test_local |>
select(segmento, n, Apredict, Bpredict) |>
DT::datatable()AUC
Si calculamos el AUC con las librerías normales no se va a tener en cuenta que tenemos datos agrupados, sino que considera cada fila como una observación. En este caso los AUC’s son como si fuera un modelo aleatorio.
pROC::auc(test_local$segmento=="Best", test_local$Apredict)## Area under the curve: 0.5035pROC::auc(test_local$segmento=="No_way", test_local$Bpredict)## Area under the curve: 0.4979Con los datos agregados se tiene por ejemplo que si en una fila n vale 1000 y la probabilidad de A es 0.2, la estimación de gente en segmento “Best” sería de 200, y podríamos calcular un test de bondad de ajuste de la Chi de Pearson, para comparar la frecuencia observada con la esperada.
\[\chi^2 = \sum_i\dfrac{(observada_i- estimada_i)^2}{estimada_i}\]
test_local |>
filter(segmento == "Best" & n > 100) |>
select(segmento, n, Apredict) |>
arrange( - Apredict) |>
mutate(A_estimate_num = Apredict * n) |>
DT::datatable()Pero seguramente, muchos están más acostumbrados a tener un AUC. Podemos tener en cuenta las frecuencias de cada fila usando la librería WeightedROC
library(WeightedROC)
# requiere que la etiqueta esté en 1 y 0
rocA <- WeightedROC::WeightedROC(test_local$Apredict,
ifelse(test_local$segmento== "Best",1,0),
weight = test_local$n)
WeightedROC::WeightedAUC(rocA)## [1] 0.6419715Y vemos que el AUC teniendo en cuenta los pesos ya no es tan malo (con tan pocas variables tampoco era esperable un auc de 0.83)
Y para el modeloB
rocB <- WeightedROC::WeightedROC(test_local$Bpredict,
ifelse(test_local$segmento == "No_way",1,0),
weight = test_local$n)
WeightedROC::WeightedAUC(rocB)## [1] 0.8499705Y vemos que para el segmento “No_way” nuestro modelo mixto no está mal del todo.
El próximo día, quiza lo haga con Stan usando brms que la sintaxis es bastante sencilla.