Antes, cuándo no había tanta capacidad de cálculo ni esa obsesión por cuántas más variables mejor, se trabajaban los datos, se seleccionaban las variables, se muestreaba o se trabajaba con los datos agregados.
De esto último sabe bastante el gran Emilio Torres, autor entre otros del paquete xkcd
Trabajar con datos agregados y con sus frecuencias es lo que hemos hecho toda la vida. Veamos un ejemplo tonto.
ejemplo <- data.frame(x1 = rep(1:3, 5),
x2 = rep(1:3, length.out=5))
ejemplo## x1 x2
## 1 1 1
## 2 2 2
## 3 3 3
## 4 1 1
## 5 2 2
## 6 3 1
## 7 1 2
## 8 2 3
## 9 3 1
## 10 1 2
## 11 2 1
## 12 3 2
## 13 1 3
## 14 2 1
## 15 3 2Tenemos 15 filas, pero en realidad podemos condensar la información en 9, que serían las combinaciones únicas
library(tidyverse)
condensado <- ejemplo %>%
group_by(x1, x2 ) %>%
count()
condensado## # A tibble: 9 x 3
## # Groups: x1, x2 [9]
## x1 x2 n
## <int> <int> <int>
## 1 1 1 2
## 2 1 2 2
## 3 1 3 1
## 4 2 1 2
## 5 2 2 2
## 6 2 3 1
## 7 3 1 2
## 8 3 2 2
## 9 3 3 1Y es exactamente la misma info, pero en menos filas. Obvio.
Veamos un ejemplo más claro con datos simulados que tengo en parquet.
library(sparklyr)
sc <- spark_connect(master = "local")
tmp <- sc %>%
spark_read_parquet(path = here::here("data/bd_pobres.parquet" ))Es un conjnto de datos con 4 variables indicando valor del cliente (1 es más valor), edad, segmento y tipo de equipamiento
tmp## # Source: spark<bd_pobres_7bdbb8aa_4b41_48bc_8c6b_6f4ff6c1acc9> [?? x 4]
## valor_cliente edad segmento tipo
## <dbl> <dbl> <chr> <chr>
## 1 3 79 No_way B
## 2 3 79 No_way B
## 3 3 79 No_way B
## 4 3 79 No_way B
## 5 3 79 No_way B
## 6 3 79 No_way B
## 7 3 79 No_way B
## 8 3 79 No_way B
## 9 3 79 No_way B
## 10 3 79 No_way B
## # … with more rowsTenemos más de 2 millones de filas. Es sólo un ejemplo, esto en un pc moderno no es un problema, pero podrían ser 200 millones
tmp %>%
count()## # Source: spark<?> [?? x 1]
## n
## <dbl>
## 1 2428386Si quisiéramos por ejemplo modelar el segmento en función del resto de variables, podríamos hacer un árbol de decisión en spark o con h2o o con otra cosa moderna. Sin embargo también podríamos pensar en ver cuántos clientes de cada tipo hay y trabajar con la tabla que tenga las distintas combinaciones y una columna que indica las veces que se repite. También podríamos trabajar con una muestra de los datos.
Y vemos que tenemos combinaciones desde 13379 casos hasta combinaciones con 1 solo caso, La combinación segmento = “No_way”, tipo = “B”, valor cliente= 8 y edad = 70 solo tiene un caso.
df_info_completa <-
tmp %>%
group_by(segmento,
tipo,
valor_cliente,
edad) %>%
count() %>%
ungroup
df_info_completa %>% arrange(desc(n))## # Source: spark<?> [?? x 5]
## # Ordered by: desc(n)
## segmento tipo valor_cliente edad n
## <chr> <chr> <dbl> <dbl> <dbl>
## 1 No_way SF 2 81 13379
## 2 No_way SF 2 85 12356
## 3 No_way SF 2 84 11657
## 4 No_way SF 2 86 11274
## 5 No_way SF 2 78 10943
## 6 No_way SF 2 87 10232
## 7 No_way SF 2 83 10158
## 8 No_way SF 2 79 10021
## 9 No_way SF 2 77 9869
## 10 No_way SF 2 80 9738
## # … with more rowsdf_info_completa %>% arrange(n)## # Source: spark<?> [?? x 5]
## # Ordered by: n
## segmento tipo valor_cliente edad n
## <chr> <chr> <dbl> <dbl> <dbl>
## 1 No_way SM 0 95 1
## 2 No_way C 6 102 1
## 3 Rec SF 6 23 1
## 4 Best C 2 103 1
## 5 Best SF 7 53 1
## 6 Best SM 6 83 1
## 7 Best SF 3 97 1
## 8 Best B 1 64 1
## 9 Neut SF 8 86 1
## 10 Best SF 7 44 1
## # … with more rowsY tendríamos un total de 9598 filas. Oye, no está mal pasar de una tabla de 2 millones a una de 9598 representando exactamente la misma información.
df_info_completa %>% count()## # Source: spark<?> [?? x 1]
## n
## <dbl>
## 1 9598Pues ya podríamos traernos la información a local y trabajar con ella
df1 <- collect(df_info_completa)
DT::datatable(df1)Y podríamos hacer nuestra segmentación utilizando la variable n como variable de frecuencia de los casos
Hagamos un segmentación sencilla
library(party)
# convertimos a factor las variables de tipo character
# The old school
# df1[sapply(df1, is.character)] <- lapply(df1[sapply(df1, is.character)],
# as.factor)
# Tidyverse
df1 <- df1 %>%
mutate(across(where(is.character),
as.factor))
df1 ## # A tibble: 9,598 x 5
## segmento tipo valor_cliente edad n
## <fct> <fct> <dbl> <dbl> <dbl>
## 1 No_way B 3 79 1612
## 2 Best SF 3 62 52
## 3 No_way SF 2 29 139
## 4 Rec C 1 43 67
## 5 Neut C 0 25 16
## 6 Neut C 4 120 1
## 7 No_way SM 2 24 800
## 8 No_way SF 5 91 8
## 9 Neut SM 1 68 51
## 10 No_way SF 5 87 11
## # … with 9,588 more rowsarbol <- ctree(segmento ~ edad + valor_cliente + tipo,
data = df1,
weights = df1$n , #
controls = ctree_control(maxdepth = 3))
arbol##
## Conditional inference tree with 8 terminal nodes
##
## Response: segmento
## Inputs: edad, valor_cliente, tipo
## Number of observations: 9598
##
## 1) tipo == {C}; criterion = 1, statistic = 848548.534
## 2) edad <= 62; criterion = 1, statistic = 53861.863
## 3) valor_cliente <= 4; criterion = 1, statistic = 25453.701
## 4)* weights = 614820
## 3) valor_cliente > 4
## 5)* weights = 411834
## 2) edad > 62
## 6) valor_cliente <= 4; criterion = 1, statistic = 13091.4
## 7)* weights = 183723
## 6) valor_cliente > 4
## 8)* weights = 77754
## 1) tipo == {B, SF, SM}
## 9) edad <= 61; criterion = 1, statistic = 144732.687
## 10) tipo == {B, SF}; criterion = 1, statistic = 96052.927
## 11)* weights = 107390
## 10) tipo == {SM}
## 12)* weights = 501076
## 9) edad > 61
## 13) valor_cliente <= 2; criterion = 1, statistic = 32631.891
## 14)* weights = 397895
## 13) valor_cliente > 2
## 15)* weights = 133894Para pintar el árbol
# una función que tengo en otro lado para modificar un
# poco como lo pinta ctree
source(here::here("utils_plot_ctree.R"))
plot(arbol,terminal_panel=altbp(arbol,ylines=1, gap=0,rot= -60))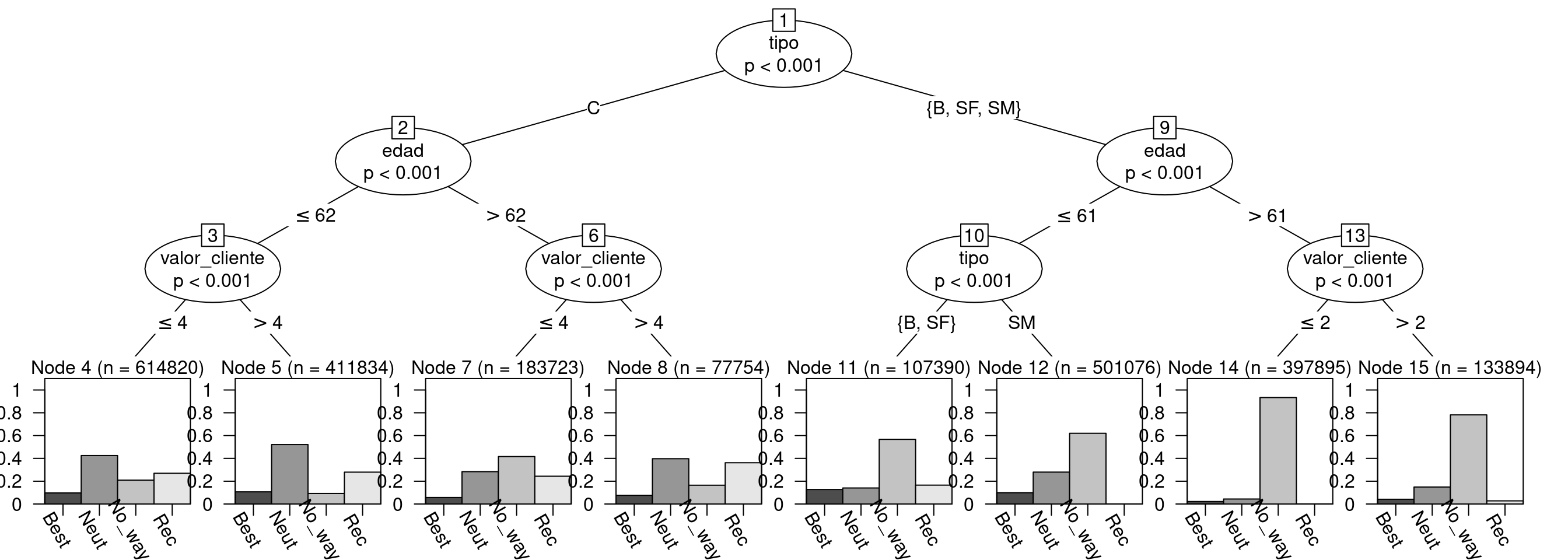
Y voilá. ya hemos hecho un modelo sobre los más de 2 millones de clientes, utilizando toda la info pero en menos de 10 mil filas. Y vemos como el tipo de equipamiento es la variable más importante, seguida de la edad. La interpretación de los segmentos la dejamos para otro día.
También podríamos considerar la variable valor cliente como categórica o discretizar la edad.
df2 <- df1 %>%
mutate(
valor_cliente = as_factor(valor_cliente),
edad_cat = as_factor(case_when(
edad <= 20 ~ "<21",
edad <= 40 ~ "21- 40",
edad <= 50 ~ "41-50",
edad <= 60 ~ "40-60",
edad > 60 ~ ">60"
))
)
arbol2 <- ctree(segmento ~ edad_cat + valor_cliente + tipo,
data = df2,
weights = df2$n , #
controls = ctree_control(maxdepth = 3))
plot(arbol2,terminal_panel=altbp(arbol,ylines=1, gap=0,rot= -60))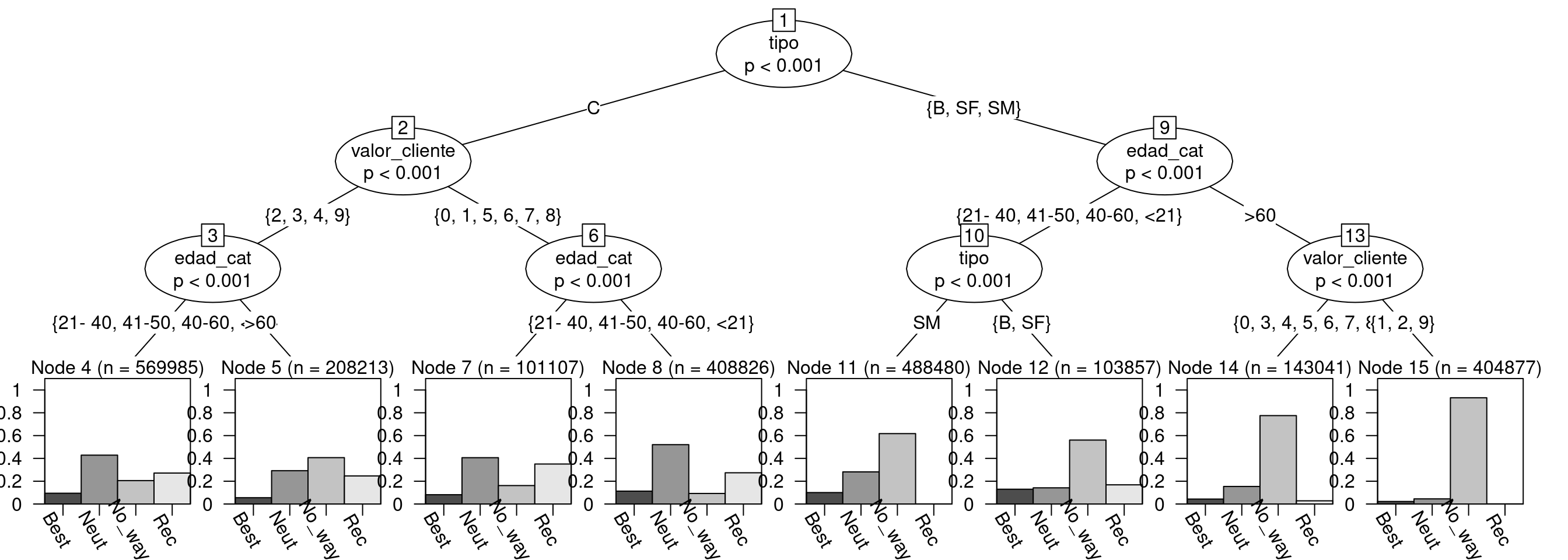
Ya que tenemos estos datos así, quizá estemos interesados en modelar la probabilidad de un segmento, quizá incluso usando Stan o lme4.
Con lme4 sería algo así.
library(lme4)
modA <- glmer(segmento == "Best" ~ (1 | edad_cat) + (1|valor_cliente) + (1 | tipo),
data = df2, family= binomial, weights= df2$n)
modB <- glmer(segmento == "No_way" ~(1 | edad_cat) + (1|valor_cliente) + (1 | tipo),
data = df2, family= binomial, weights= df2$n) Y ver el modelo y efectos aleatorios
summary(modA) ## Generalized linear mixed model fit by maximum likelihood (Laplace
## Approximation) [glmerMod]
## Family: binomial ( logit )
## Formula: segmento == "Best" ~ (1 | edad_cat) + (1 | valor_cliente) + (1 |
## tipo)
## Data: df2
## Weights: df2$n
##
## AIC BIC logLik deviance df.resid
## 1323329.0 1323357.6 -661660.5 1323321.0 9594
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -25.667 -2.415 -0.814 2.158 112.275
##
## Random effects:
## Groups Name Variance Std.Dev.
## valor_cliente (Intercept) 0.06517 0.2553
## edad_cat (Intercept) 0.38928 0.6239
## tipo (Intercept) 0.01492 0.1222
## Number of obs: 9598, groups: valor_cliente, 10; edad_cat, 5; tipo, 4
##
## Fixed effects:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -2.0959 0.2987 -7.016 2.28e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1ranef(modA)## $valor_cliente
## (Intercept)
## 0 0.40814889
## 1 0.08097667
## 2 -0.25006647
## 3 -0.22331683
## 4 -0.30648824
## 5 -0.15176063
## 6 0.05926169
## 7 0.20797030
## 8 0.26778673
## 9 -0.09214299
##
## $edad_cat
## (Intercept)
## >60 -0.904157563
## 21- 40 0.307420538
## 41-50 -0.001555638
## 40-60 -0.334084647
## <21 0.934582147
##
## $tipo
## (Intercept)
## B -0.15014769
## C 0.14785788
## SF -0.01783835
## SM 0.02021269
##
## with conditional variances for "valor_cliente" "edad_cat" "tipo"sjPlot::plot_model(modA, type = "re")## [[1]]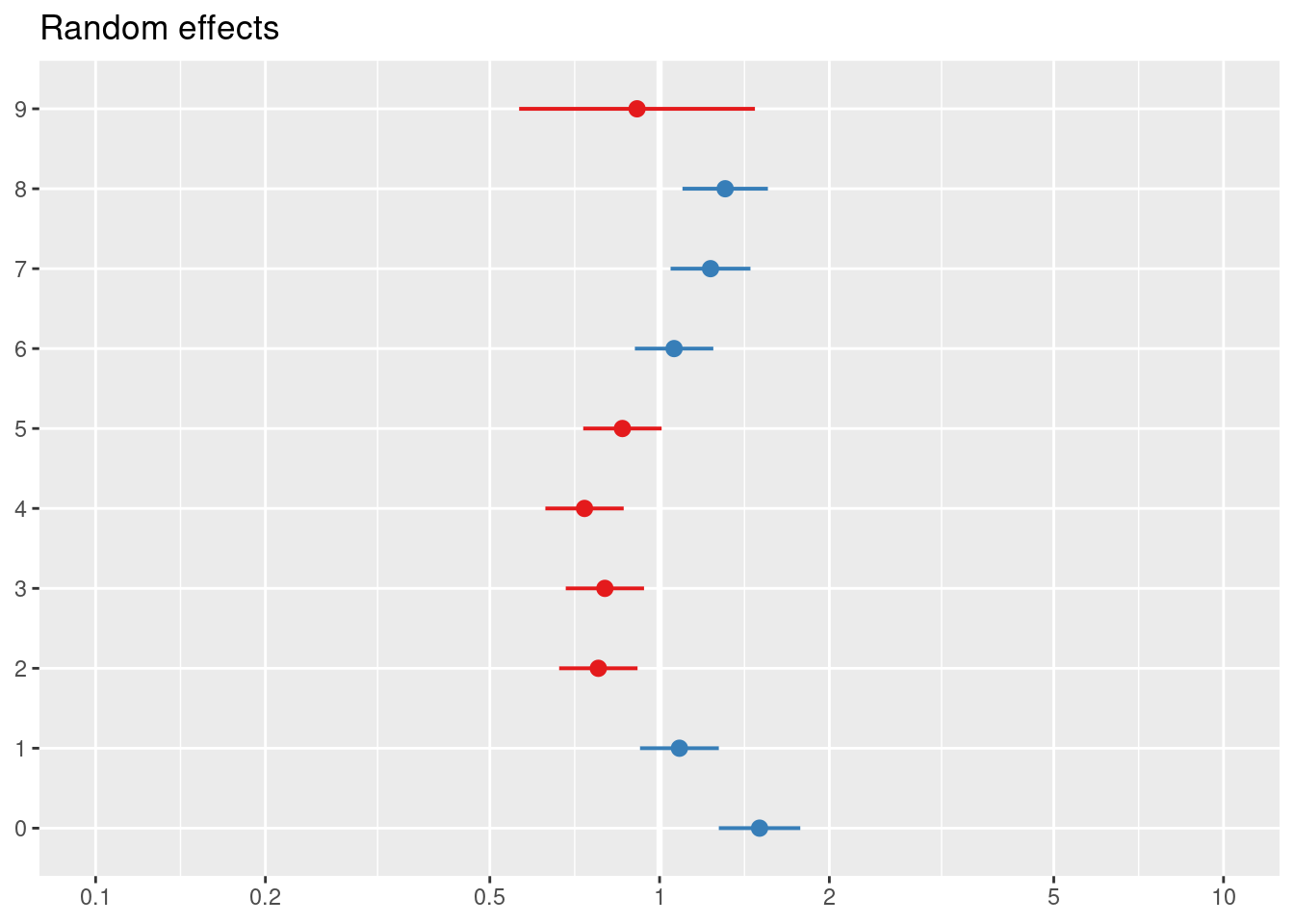
##
## [[2]]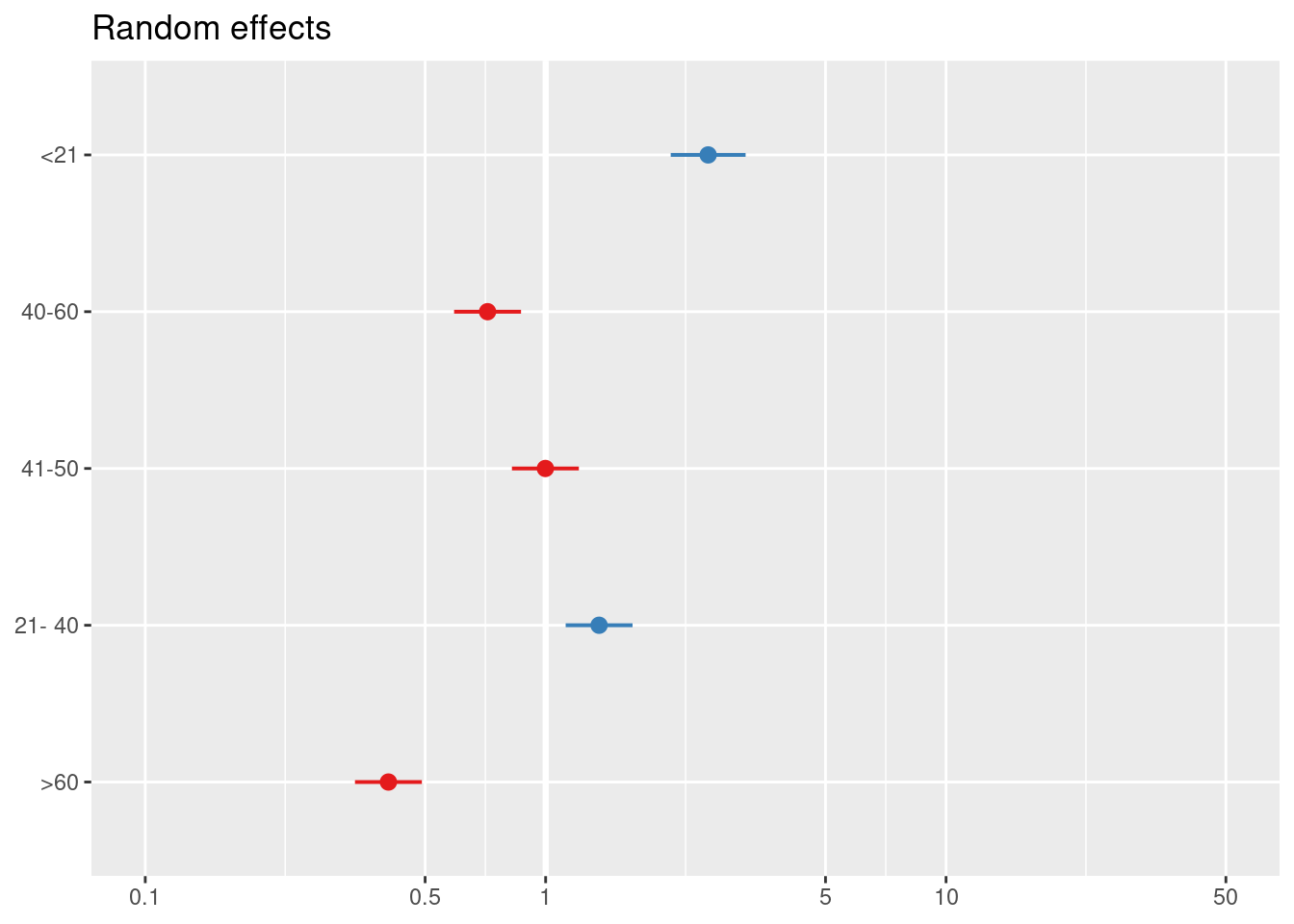
##
## [[3]]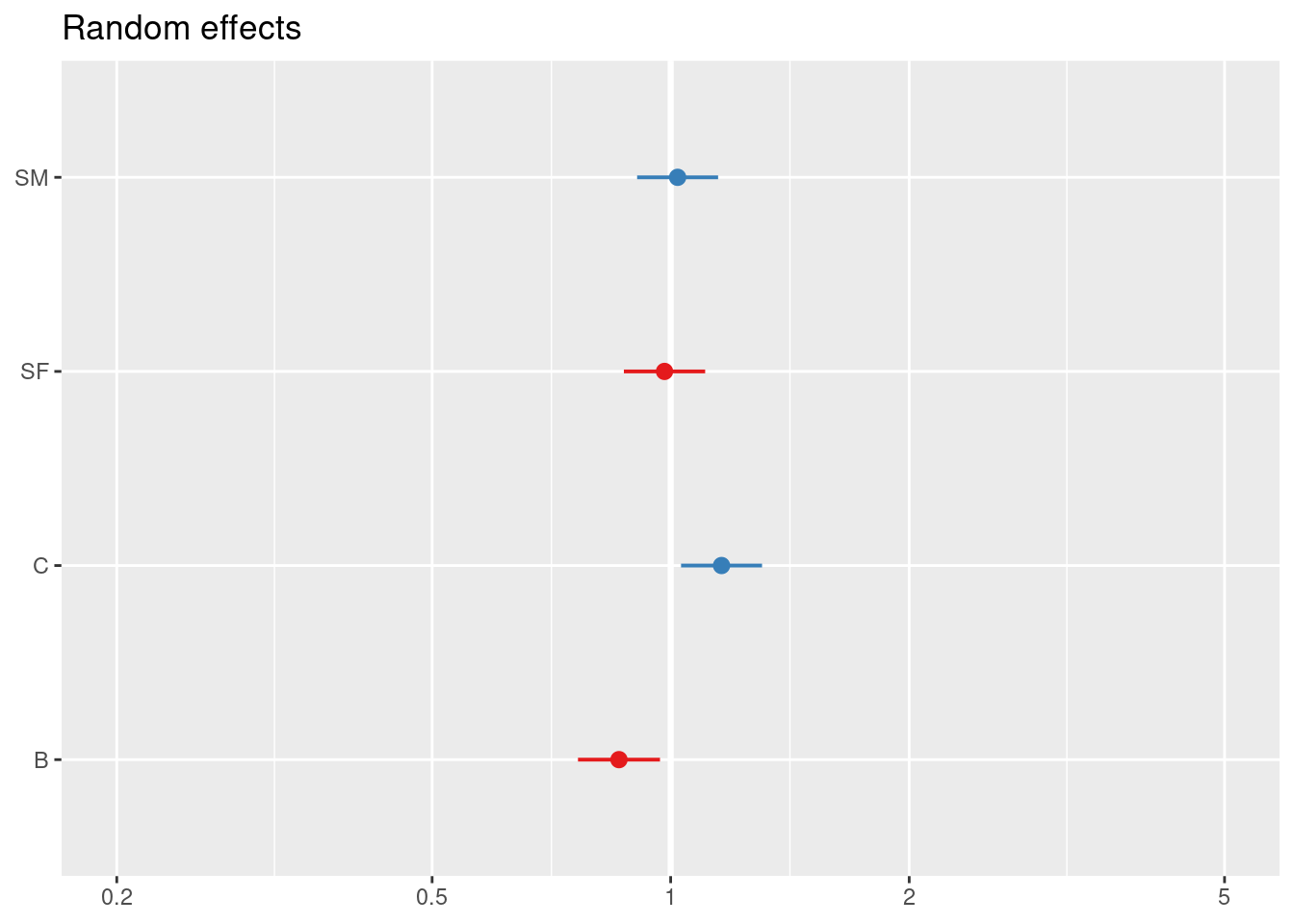
Y hasta aquí, el próximo post en vez de trabajar con toda la información partiremos los datos en train y test antes de agregar y traer a local. Veremos el ajuste con un modelo mixto con glmer y calcularemos los AUC’s, pero teniendo en cuenta que tenemos los datos con variable de frecuencia.