El título de la entrada, sobre todo lo de la parte de “estilo compadre” viene de mis tiempos en consultoría, y tiene que ver con la necesidad de dar soluciones subóptimas a problemas acuciantes. Otra de mis frases, de la que puede que se acuerden Boris, Laura y Lourdes fue la de “si me das madera te hago un troncomóvil, no un ferrari”, lo cual es el equivalente a GIGO de toda la vida, pero a mi estilo.
Vamos al lío, últimamente ando estudianddo estadística bayesiana con el excelente material que pone a disposición de todo el mundo, y gratis, Aki Vehtari en este sitio Curso BDA3. Aki Vehtari es uno de los autores junto con Gelman y otros del libro Bayesian Data Analysis.
En la página 48 y siguientes tienen un ejemplo de como realizar inferencia bayesiana para el ratio muertes por cáncer usando un modelo básico Poisson-Gamma. Pero lo interesante es que comentan como construir una priori a partir de los datos, y que la forma en que lo hacen en este ejemplo puede considerarse una aproximación a como se construye en los modelos jerárquicos.
Total, que dado que en mi pueblo han aumentado, por desgracia, los casos y nos han confinado perimetralmente, voy a hacer el ejercicio de utilizar los datos del área sanitaria granada nordeste y adaptar el ejemplo.
Aviso que mi conocimiento de estadística bayesiana es limitado y muy probablemente puede que haga algo mal. Estoy aprendiendo, jejej.
Datos
En primer lugar los datos por municipios vienen aqui. Y bueno, estaría bien que estuvieran un poco mejor organizados, puesto que solo puedes bajarte los últimos datos actualizados, no hay serie histórica por municipio, o al menos yo no la he encontrado.
Después de bajarme el excel al final me quedo solo con los datos de los municipios del área sanitaria Granada Nordeste.
library(tidyverse)## ── Attaching packages ─────────────────────────────────────── tidyverse 1.3.0 ──## ✓ ggplot2 3.3.3 ✓ purrr 0.3.4
## ✓ tibble 3.1.0 ✓ dplyr 1.0.5
## ✓ tidyr 1.1.3 ✓ stringr 1.4.0
## ✓ readr 1.4.0 ✓ forcats 0.5.1## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## x dplyr::filter() masks stats::filter()
## x dplyr::lag() masks stats::lag()g_nordeste <- read_csv(here::here("data/g_nordeste_20210326.csv"))##
## ── Column specification ────────────────────────────────────────────────────────
## cols(
## lugar_de_residencia = col_character(),
## poblacion_miles = col_double(),
## confirmados_pdia_14_dias = col_double()
## )g_nordeste## # A tibble: 46 x 3
## lugar_de_residencia poblacion_miles confirmados_pdia_14_dias
## <chr> <dbl> <dbl>
## 1 Alamedilla 0.569 0
## 2 Albuñán 0.409 0
## 3 Aldeire 0.63 0
## 4 Alicún de Ortega 0.471 0
## 5 Alquife 0.580 0
## 6 Baza 20.4 27
## 7 Beas de Guadix 0.329 0
## 8 Benalúa 3.31 11
## 9 Benamaurel 2.26 4
## 10 Calahorra (La) 0.668 0
## # … with 36 more rowsY podríamos contruir las tasas brutas por cada mil habitantes.
g_nordeste <- g_nordeste %>%
mutate(tasa_bruta = confirmados_pdia_14_dias / poblacion_miles)
g_nordeste %>%
arrange(-tasa_bruta)## # A tibble: 46 x 4
## lugar_de_residencia poblacion_miles confirmados_pdia_14_dias tasa_bruta
## <chr> <dbl> <dbl> <dbl>
## 1 Cogollos de Guadix 0.642 17 26.5
## 2 Purullena 2.31 29 12.6
## 3 Cortes de Baza 1.84 22 11.9
## 4 Peza (La) 1.17 8 6.86
## 5 Dólar 0.628 4 6.37
## 6 Zújar 2.54 15 5.90
## 7 Cúllar 4.09 23 5.62
## 8 Cuevas del Campo 1.74 6 3.44
## 9 Benalúa 3.31 11 3.32
## 10 Huéneja 1.17 3 2.56
## # … with 36 more rowsBueno, y vemos que mi pueblo, está el tercero con mayor tasa con 12.58 por 1000 habitantes o 1258 por cada 100 mil (si revisan la situación el próximo martes posiblemente cierren la activad esencial).
Inferencia
Bueno, pues podríamos considerar que los casos en un municipio \(y_i\) la verosimilitud sería de la forma
\[y_i \sim Poisson(X_i\cdot\theta_i)\]
dónde \(X_i\) sería la población en miles y \(\theta_i\) la tasa por cada 1000 habitantes.
Ahora el tema para hacer inferencia bayesiana es especificar la prior, y como comentan en el libro podríamos construir la prior utilizando los datos. El número de casos sigue una “predictive distribution” binomial negativa y con un poco de álgebra llegan a igualar la media y varianza de las tasas brutas y obtener los parámetros de esa binomial negativa. Aquí es cuándo llega lo de “estilo compadre”, en vez de considerar la binomial negativa, yo voy a ajustar una Gamma a las tasas brutas y calculo el \(\alpha\) y \(\beta\) de la gamma por el método de los momentos.
Elegir una Gamma como Prior es en parte porque es distribución conjugada de la Poisson y la posterior se obtiene directamente.
Sin más, sería resolver estas ecuaciones
\[E[\text{tasas brutas}] = \dfrac{\alpha_{prior}}{\beta_{prior}}\] \[Var[\text{tasas brutas}] = \dfrac{\alpha_{prior}}{\beta_{prior}^{2}}\]
Despejando
media = mean(g_nordeste$tasa_bruta)
cuasivarianza = var(g_nordeste$tasa_bruta)
(beta = media/cuasivarianza)## [1] 0.1028402(alpha = media* beta)## [1] 0.2312364Por lo que usaremos como prior una \(Gamma(0.10, 0.23)\), que parece un poco débil, seguramente porque las tasas brutas son muy diferentes entre los municipios.
Comparando la densidad de las tasas brutas con la densidad de la priori no parece mala elección
# repito 10 veces cada tasa para tner suficients puntos para ver la densidad estimada
df <- data.frame(raw_thetas = rep(g_nordeste$tasa_bruta,10),
simulados = rgamma(nrow(g_nordeste)*10, alpha, beta) )
df %>%
ggplot(aes(x=raw_thetas)) +
geom_density(size = 1) +
geom_density(aes(x=simulados), col = "darkred", linetype=2, size = 1)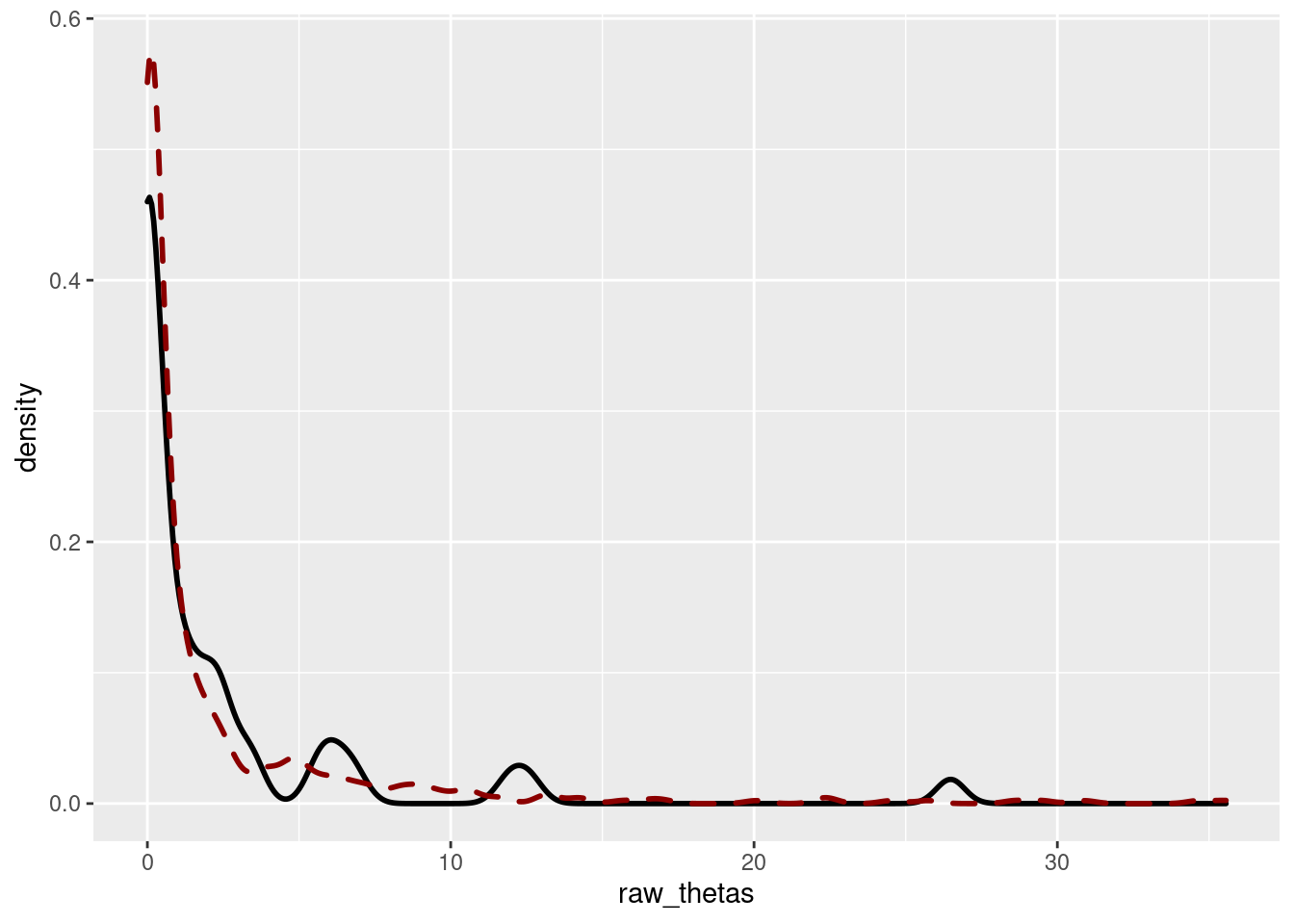
Y ya sólo quedaría calcular la posterior para cada municipio. Que sería de esta forma
\[P\left( \theta_i\mid data \right) \sim \text{Gamma}(\alpha_{prior} + y_i, \beta_{prior} + x_i)\] Dónde \(y_i\) es el número de casos en los últimos 14 días en cada municipio y \(x_i\) los expuestos, es decir, la población (en miles) en cada municipio. Con esto ya podemos calcular, y añadimos también los intervalos de credibilidad
g_nordeste <- g_nordeste %>%
mutate(
posterior_a = alpha + confirmados_pdia_14_dias,
posterior_b = beta + poblacion_miles,
posterior_mean = posterior_a/posterior_b,
lb = qgamma(.025, posterior_a, posterior_b),
ub = qgamma(.025, posterior_a, posterior_b, lower.tail = FALSE)
) Y si vemos los datos de mi pueblo y de alguno más.
g_nordeste %>%
filter(lugar_de_residencia %in% c("Cortes de Baza","Castilléjar", "Baza","Castril", "Benamaurel", "Zújar")) %>%
select(lugar_de_residencia, poblacion_miles,
confirmados_pdia_14_dias,
tasa_bruta,
posterior_mean) %>%
arrange(-posterior_mean)## # A tibble: 6 x 5
## lugar_de_residen… poblacion_miles confirmados_pdia_… tasa_bruta posterior_mean
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 Cortes de Baza 1.84 22 11.9 11.4
## 2 Zújar 2.54 15 5.90 5.75
## 3 Benamaurel 2.26 4 1.77 1.79
## 4 Baza 20.4 27 1.32 1.33
## 5 Castilléjar 1.32 1 0.757 0.865
## 6 Castril 2.02 0 0 0.109Pues no varía mucho la posterior con respecto a a la bruta. Puede deberse a dos motivos, uno, que al tener gran variabilidad las tasas brutas en los municipios considerados la información que comparten es poca comparada con la información específica que aporta cada municipio y la verosimilitud se impone a la prior y por otro lado, al no haber hecho full bayesian para estimar la prior , hemos utilizado los datos de los muncipios dos veces, una para obtener los parámetros de la prior y otra para la posterior, lo que puede llevar a sobreajuste. En los modelos jerárquicos bien estimados (y no al estilo compadre), si se estima bien, pero esto es una aproximación para entender un poco la lógica que hay debajo.
Y ya solo falta pintar .
g_nordeste %>%
ggplot(aes(x=reorder(lugar_de_residencia, posterior_mean), y = posterior_mean)) +
geom_point(color = "darkred", size = rel(2)) +
geom_errorbar(aes(ymin = lb , ymax = ub)) +
coord_flip() +
labs(x = "municipio", y = "Tasa x 1000 habitantes")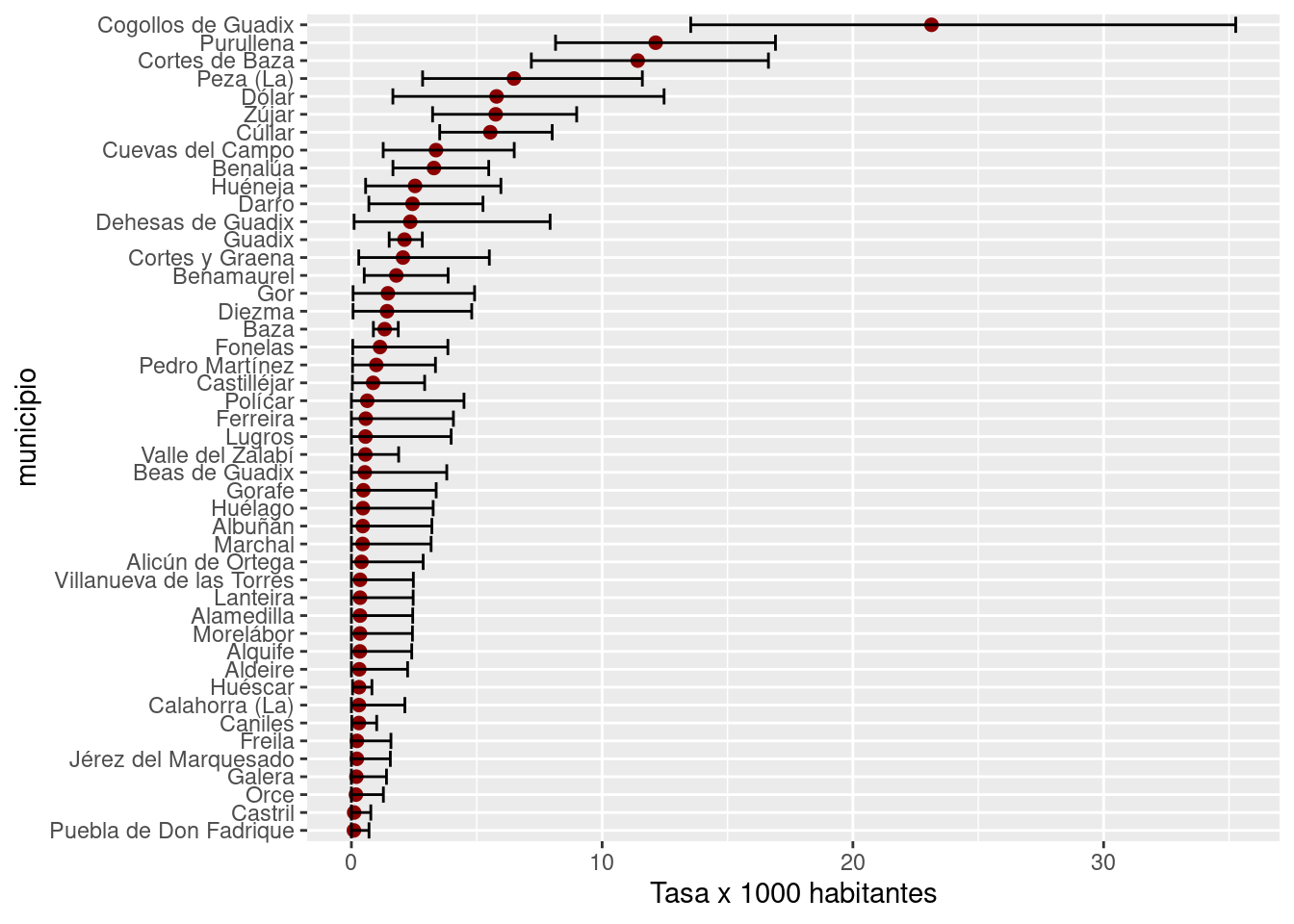
Los intervalos de credibilidad más pequeños se corresponden con los municipios con mayor población. A la vista de estos datos, se deberían usar este tipo de estimadores (bien hechos) sobre todo para estimar en municipios con una población menor, y no tomar decisiones basadas en una estimación puntual.
Coda. Utilizando un glmer con family poisson (o con binomial si se modela la tasa directamente) con efecto aleatorio el lugar de residencia se obtienen prácticamente los mismos resultados