Hoy vamos a darle una (pequeña) vuelta de tuerca al tema de la reducción de dimensiones ( y por ende la codificación ) con variables categóricas y ordinales.
Aunque puede que muchos no lo sepan, existen dos escuelas derivadas de lo que Tukey llamaba el análisis exploratorio de datos, a saber, la francesa y la holandesa.
La francesa con exponentes como Jean-Paul Benzécri, Saporta o Lebart, resuelven el problema de proyectar las relaciones entre variables categóricas en un hiperplano de menor dimensión de forma analítica.
Por otro lado tenemos la escuela holandesa, que se diferencia de la escuela francesa en la forma de solucionar el problema, ya que la escuela holandesa llega a la solución mediante métodos de optimización numérica. Representantes de esta escuela son Jan de Leeuw o Patrick Mair, que entre otros forman parte del grupo de teoría de datos más conocidos por su pseudónimo “Albert Gifi” en honor al criado de Galton.
En el estupendo artículo de Francois Husson sobre la influencia de Jan de Leeuw en la escuela francesa de análisis de datos, cuenta la relación entre el análisis de correspondencias múltiple (MCA) desarrollado por la escuela francesa y el análisis de homogeneidad por als (homals), de la escuela holandesa.
Para el que quiera profundizar más, recomiendo el libro de Patrick Mair, Modern Psycometrics with R, dónde viene de todo, desde teoría clásica del test, análisis factorial exploratorio y confirmatorio, modelos de ecuaciones estructurales, modelos de preferencia, independent component analysis, mca, homals, multidimensional scaling , análisis de datos funcionales, en fin, de todo.
En el capítulo 8 del libro de Mair se describe muy bien como es su aproximación al problema que consiste básicamente en encontrar una cuantificación de las filas y en una cuantificación de las categorías de las variables (optimal scaling).
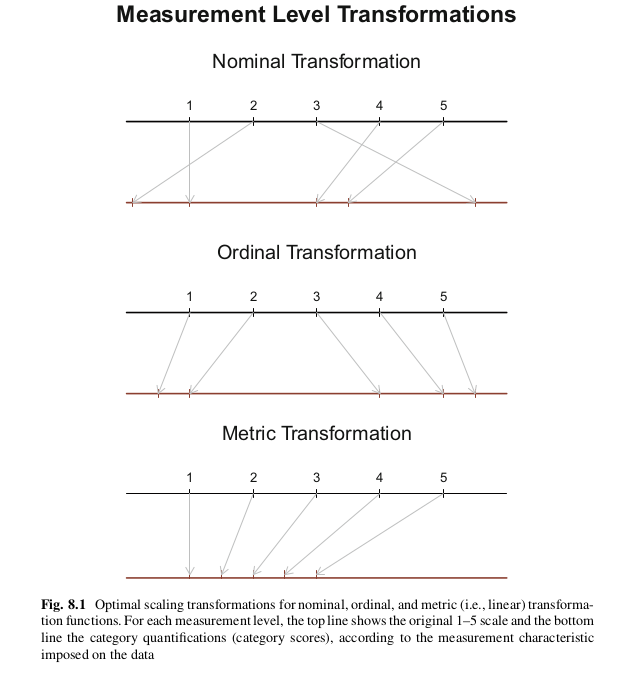
Bien, los métodos Gifi, se basan en minimizar una expresión similar a esta
\[ \sigma(X, Y_1, \ldots, Y_m) = \sum_{j=1}^{m}\text{tr}(\boldsymbol{X} - \boldsymbol{G_j\,Y_j} )^\mathsf{T}(\boldsymbol{X} - \boldsymbol{G_j\,Y_j} ) \] dónde \(G_j\) es la matriz indicadora para cada variable \(j\), de dimensión \(n\times k_j\) , dónde \(n\) es el número de observaciones y \(k_j\) el número de categorías de la variable categórica j-ésima. Cada variables categórica \(j\) está asociada con una matriz \(Y_j\) de dimensión \(k_j\times p\) que representa la cuantificación de cada categoría en las p dimensiones que se quieren obtener. Y por último la matriz \(X\) de dimensión \(n\times p\) representa los object scores que no es más que las puntuaciones en la estructura factorial de dimensión \(p\) de las \(n\) filas del conjunto de datos.
Como vemos es un problema de optimización, se quiere minimizar el lado derecho de la ecuación, que básicamente es una suma de cuadrados, es una doble optimización porque por un lado se quiere encontrar la representación de las filas en el espacio p (asimilable a un PCA) y por otro encontrar la mejor cuantificación de las variables categóricas. Esa última parte es a la que los integrantes del grupo Gifi llaman optimal scaling. Para minimizar la expresión anterior, utilizan ALS (alternative least squares).
Veamos ahora la aplicación de esta técnica al mismo conjunto de datos que venimos utilizando
library(Gifi)
datos <- readRDS("../../data/science.rds")non_linear_pca <- princals(datos, ndim = 3, ordinal = TRUE) # principal components analisys, with alssummary(non_linear_pca)##
## Loadings (cutoff = 0.1):
## Comp1 Comp2 Comp3
## Environment 0.651 0.429
## Technology 0.660 0.453 -0.101
## Industry 0.695 0.356
## Future 0.493 -0.553 0.388
## Benefit 0.288 -0.618 -0.486
## Comfort 0.432 -0.501 -0.522
## Work 0.278 -0.484 0.677
##
## Importance (Variance Accounted For):
## Comp1 Comp2 Comp3
## Eigenvalues 1.9354 1.6854 1.1342
## VAF 27.6491 24.0768 16.2031
## Cumulative VAF 27.6500 51.7300 67.9300En el objeto tenemos diferentes resultados. Por un lado tenemos los transform que se corresponden con el optimal scaling es decir, la forma en que ha codificado cada categoría de cada variable
head(non_linear_pca$transform)## Comfort Environment Work Future Technology Industry
## 1 0.036206806 0.07230200 0.101468821 -0.009079003 0.07175648 -0.04238874
## 2 0.002943972 0.07230200 0.006469192 -0.009079003 -0.02328406 -0.04238874
## 3 0.002943972 -0.04050877 -0.040329478 -0.050465165 0.07175648 0.06018155
## 4 0.002943972 -0.03058008 -0.040329478 -0.050465165 0.07175648 0.06018155
## 5 0.002943972 -0.04050877 0.101468821 0.076628333 -0.04941027 -0.04238874
## 6 0.036206806 -0.03058008 0.101468821 -0.009079003 -0.02328406 0.06018155
## Benefit
## 1 -0.002163702
## 2 0.010537115
## 3 0.010537115
## 4 0.010537115
## 5 -0.206624740
## 6 0.010537115Y vemos que la categoría agree en la variable Comfort la ha codificado con el valor 0.0029, y la strongly agree con el valor 0.0036
head(datos)## Comfort Environment Work Future Technology
## 1 strongly agree strongly agree strongly agree agree strongly agree
## 2 agree strongly agree agree agree agree
## 3 agree disagree disagree disagree strongly agree
## 4 agree agree disagree disagree strongly agree
## 5 agree strongly disagree strongly agree strongly agree disagree
## 6 strongly agree agree strongly agree agree agree
## Industry Benefit
## 1 agree disagree
## 2 agree agree
## 3 strongly agree agree
## 4 strongly agree agree
## 5 agree strongly disagree
## 6 strongly agree agreeTambién tenemos la matriz de correlación inducida
non_linear_pca$rhat## Comfort Environment Work Future Technology
## Comfort 1.00000000 0.069404402 0.056884551 0.24184038 0.062590630
## Environment 0.06940440 1.000000000 -0.007068416 0.06896166 0.446698147
## Work 0.05688455 -0.007068416 1.000000000 0.41223214 -0.039643944
## Future 0.24184038 0.068961662 0.412232143 1.00000000 0.025127731
## Technology 0.06259063 0.446698147 -0.039643944 0.02512773 1.000000000
## Industry 0.07027680 0.400503291 0.033788170 0.14510083 0.445635418
## Benefit 0.41522167 -0.058500244 0.096205075 0.22566741 -0.006006693
## Industry Benefit
## Comfort 0.07027680 0.415221675
## Environment 0.40050329 -0.058500244
## Work 0.03378817 0.096205075
## Future 0.14510083 0.225667408
## Technology 0.44563542 -0.006006693
## Industry 1.00000000 -0.032364297
## Benefit -0.03236430 1.000000000Con esta matriz podríamos usarla de input para un pca o un fa estándar, si lo hacemos vemos que es bastante parecido al que salía utilizando las correlaciones policóricas
library(psych)
diagram(fa(non_linear_pca$rhat, nfactors = 3))## Loading required namespace: GPArotation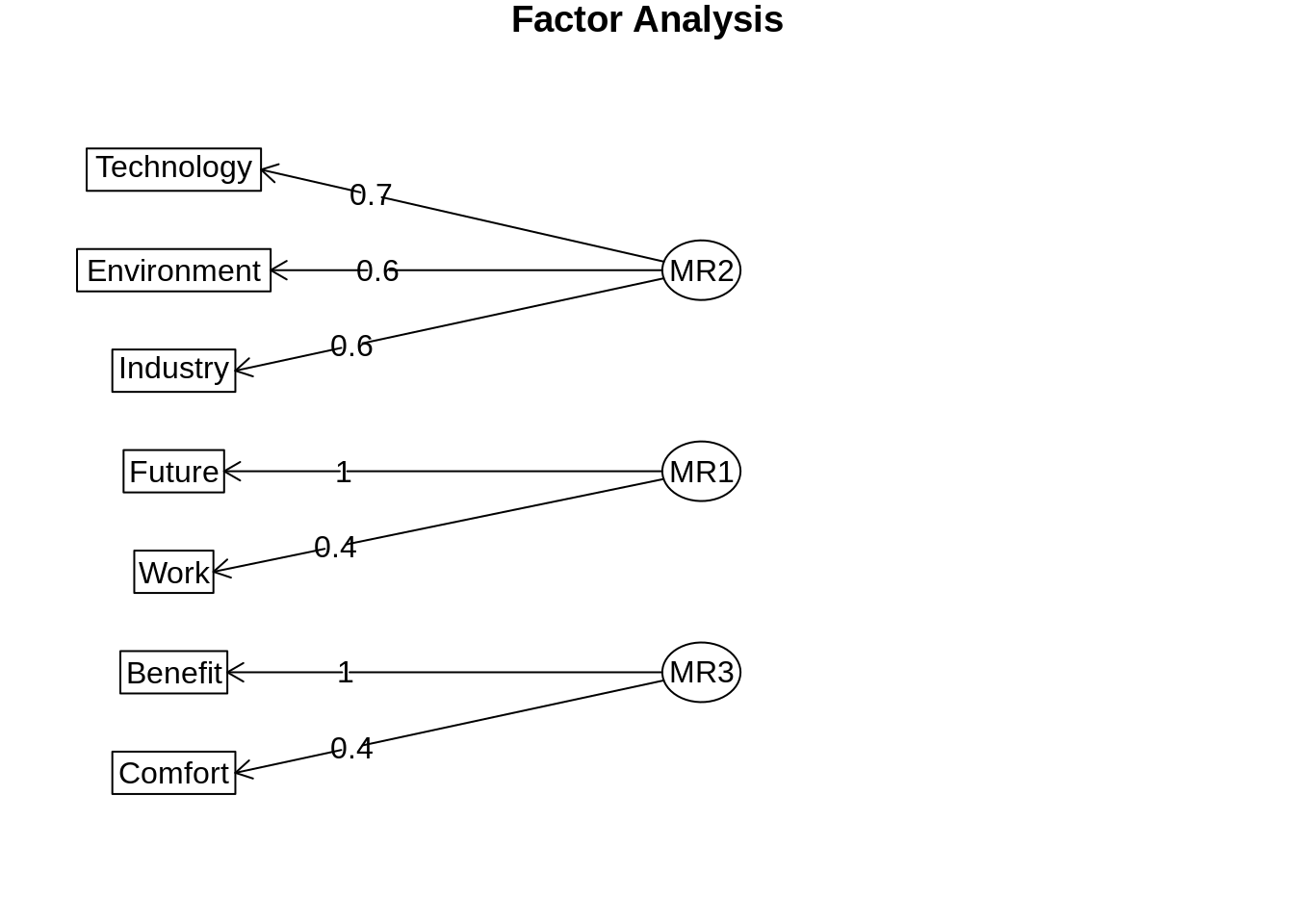
Por otra parte tenemos los autovalores
non_linear_pca$evals## [1] 1.9354363 1.6853783 1.1342154 0.6048395 0.6014854 0.5345614 0.5040837Tenemos también las puntuaciones de las filas en la estructura factorial.
head(non_linear_pca$objectscores)## D1 D2 D3
## 1 1.06516050 -0.160525856 0.6373183
## 2 0.03985905 -0.008157353 -0.1209814
## 3 0.30665165 0.887267528 -0.9770977
## 4 0.37223871 0.936297246 -0.9776115
## 5 -0.82611294 -0.225707817 3.4756697
## 6 0.51260624 -0.841697990 0.8431892Las cuantificaciones de cada categoría en cada dimensión, que es diferente de la transformación de la categoría, esto es la proyección de esas transformaciones en la estructura factorial
non_linear_pca$quantifications## $Comfort
## D1 D2 D3
## [1,] -0.167024465 0.193559780 0.201626389
## [2,] -0.058550616 0.067852601 0.070680360
## [3,] 0.002544824 -0.002949122 -0.003072027
## [4,] 0.000000000 0.000000000 0.000000000
## [5,] 0.015648915 -0.018135071 -0.018890850
##
## $Environment
## D1 D2 D3
## [1,] -0.02638816 -0.01739241 1.011129e-04
## [2,] -0.01293547 -0.00852575 4.956548e-05
## [3,] -0.03984086 -0.02625906 1.526603e-04
## [4,] 0.00000000 0.00000000 0.000000e+00
## [5,] 0.04709886 0.03104280 -1.804711e-04
##
## $Work
## D1 D2 D3
## [1,] -0.024970331 0.043402642 -0.060728093
## [2,] -0.026046019 0.045272369 -0.063344177
## [3,] 0.003600459 -0.006258205 0.008756353
## [4,] 0.000000000 0.000000000 0.000000000
## [5,] 0.028236474 -0.049079748 0.068671384
##
## $Future
## D1 D2 D3
## [1,] -0.063932619 0.07168965 -0.050334629
## [2,] -0.040790877 0.04574009 -0.032114962
## [3,] -0.008948413 0.01003414 -0.007045153
## [4,] 0.000000000 0.00000000 0.000000000
## [5,] 0.037763068 -0.04234491 0.029731146
##
## $Technology
## D1 D2 D3
## [1,] -0.03262656 -0.02239101 0.004996798
## [2,] -0.03450328 -0.02367897 0.005284221
## [3,] -0.03074983 -0.02110305 0.004709375
## [4,] 0.00000000 0.00000000 0.000000000
## [5,] 0.04738219 0.03251753 -0.007256642
##
## $Industry
## D1 D2 D3
## [1,] -2.945496e-02 -1.507179e-02 -3.370967e-03
## [2,] -1.619427e-17 2.024283e-17 6.072850e-18
## [3,] -5.890993e-02 -3.014358e-02 -6.741935e-03
## [4,] 0.000000e+00 0.000000e+00 0.000000e+00
## [5,] 4.181878e-02 2.139822e-02 4.785941e-03
##
## $Benefit
## D1 D2 D3
## [1,] -0.059597532 0.12769143 0.10036142
## [2,] -0.007326687 0.01569788 0.01233804
## [3,] 0.006078517 -0.01302360 -0.01023614
## [4,] 0.000000000 0.00000000 0.00000000
## [5,] 0.009325381 -0.01998021 -0.01570381Y entre otras cosas también tenemos los loadings que sería la contribución de cada variable a cada dimensión
non_linear_pca$loadings## D1 D2 D3
## Comfort 0.4318184 -0.5007726 -0.522173943
## Environment 0.6514179 0.4293499 -0.002499057
## Work 0.2783044 -0.4836307 0.676806699
## Future 0.4928160 -0.5525992 0.387984605
## Technology 0.6603170 0.4531618 -0.101158965
## Industry 0.6948770 0.3555611 0.079525057
## Benefit 0.2879627 -0.6178341 -0.486197461Así, por ejemplo vemos que las variables Environment, Technology e Industry son los que tienen una mayor puntuación (en valor absoluto) a la primera dimensión. y vemos que la categoría 4 de Industria (“strongly agree”) tiene un valor positvo en esa dimensión así como Technology y Environment. Básicamente, los individuos que están muy de acuerdo con las afirmaciones siguientes, tendrán una puntuación muy alta en la primera dimensión.
Afirmaciones
Environment: Scientific and technological research cannot play an important role in protecting the environment and repairing it.
Technology: New technology does not depend on basic scientific research.
Industry: Scientific and technological research do not play an important role in industrial development.
Lo interesante de esta técnica es que por un lado nos devuelve una codificación de las variables categóricas (ordinales en este caso) en dimensión 1 y por otro hace la reducción de dimensiones. Nosotros podríamos utilizar la codificación por “optimal scaling” como nuestra “codificación de categóricas” o usar las dimensiones obtenidas, en este caso 3.
La libreria Gifi tiene también para sacar algunos gráficos interesantes
plot(non_linear_pca)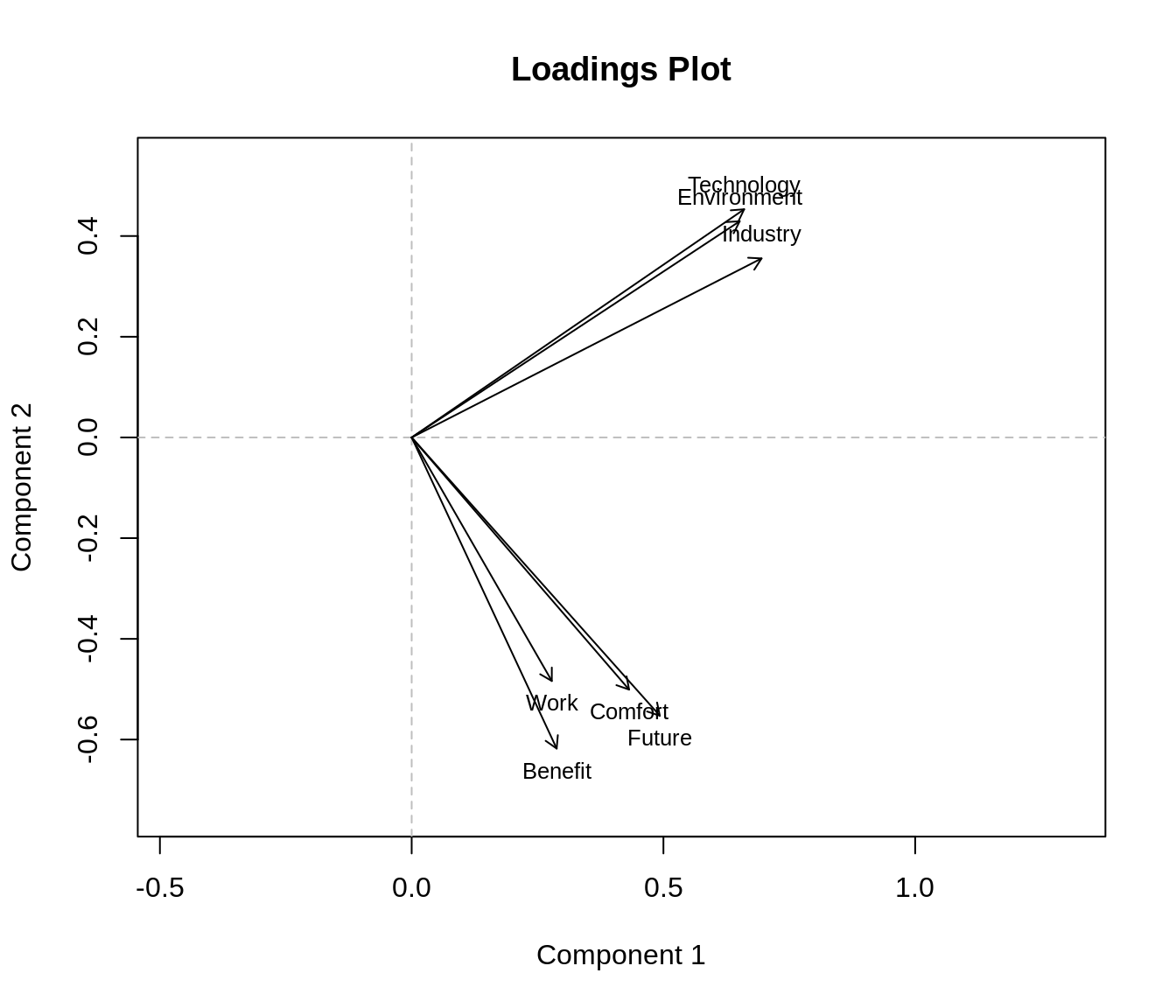
plot(non_linear_pca, plot.type = "transplot")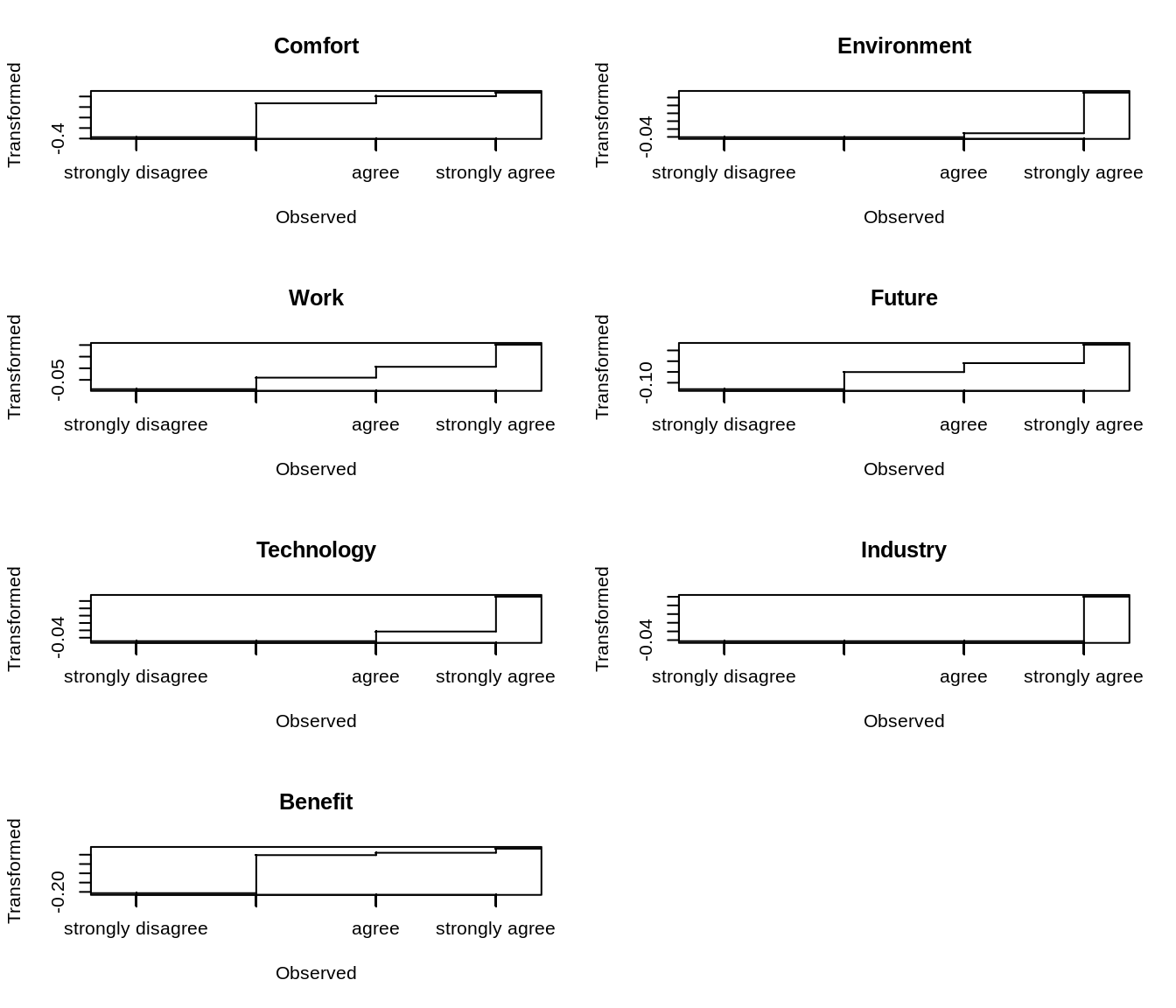
Dejo para el lector (si hay alguno) la utilización de la función homals del mismo paquete, que es una función más general y permite hacer análisis de correspondencias múltiples utilizando este marco de análisis.
Nota: En este marco “Gifi Methods” entrarían como casos particulares el PCA, MCA, Conjoint Analysis, análisis de correlaciones canónicas, análisis discriminante o la regresión múltiple.
comments powered by Disqus