Volviendo al ejemplo de lo de las proporciones pequeñas, se trataba básicamente de que se tenía una población con una prevalencia de cierto evento del 4 x 1000 más o menos y en post anteriores veíamos cómo calcular tamaños de muestra y tal para ver cómo detectar un incremento de un 15% en esa proporción.
Ahora vamos a suponer que tenemos una población de 1.5 millones, pero que hay 5 grupos diferenciados, con prevalencias del 6, 5, 4, 3 y 2 por mil respectivamente y todos del mismo tamaño. Simulemos dicha población
set.seed(155)
gr1 <- rbinom(n = 3E5, size = 1, prob = 0.006)
gr2 <- rbinom(n = 3E5, size = 1, prob = 0.005)
gr3 <- rbinom(n = 3E5, size = 1, prob = 0.004)
gr4 <- rbinom(n = 3E5, size = 1, prob = 0.003)
gr5 <- rbinom(n = 3E5, size = 1, prob = 0.002)
pop <- data.frame(grupo = rep(letters[1:5],each= 3E5),
evento = c(gr1,gr2,gr3,gr4,gr5))Veamos 30 casos al azar.
pop[sample(1:nrow(pop), 30),]## grupo evento
## 92075 a 0
## 424873 b 0
## 1201923 e 0
## 1159523 d 0
## 830570 c 0
## 546477 b 0
## 1120381 d 0
## 613315 c 0
## 485130 b 0
## 52029 a 0
## 619858 c 0
## 590223 b 0
## 1034676 d 0
## 1153071 d 0
## 1266210 e 0
## 502866 b 0
## 99782 a 0
## 1388671 e 0
## 26049 a 0
## 971047 d 0
## 709908 c 0
## 376850 b 0
## 487569 b 0
## 365383 b 0
## 376533 b 0
## 1094390 d 0
## 873846 c 0
## 514258 b 0
## 1423814 e 0
## 730321 c 0Comprobamos la prevalencia en la población total y por grupos
mean(pop$evento)## [1] 0.003958with(pop,tapply(evento, grupo, mean))## a b c d e
## 0.005836667 0.004963333 0.004213333 0.002846667 0.001930000Supongamos ahora que encuentro un grupo por ahí del mismo tamaño (300k) con una prevalencia igual al mejor grupo que tengo, es decir, del 6 x 1000 y que la gente de marketing me cree y me deja que quite 300K con peor prevalencia y que los sustituya con mi grupo. ¿Cuánto sería la mejora de la prevalencia en esa nueva población?
Simulemos
pop_new <- pop
pop_new$evento[pop_new$grupo=="e"] <- rbinom(n = 3E5, size = 1, prob = 0.006)
mean(pop_new$evento)## [1] 0.004748667mean(pop_new$evento)/mean(pop$evento)## [1] 1.199764La mejora sería del 19.9764191, % pero, ¿es porque he tenido suerte?. Si todos los meses encontrara un grupo así de majo, ¿en qué valores de mejora me estaría moviendo?
Simulemos 100 realizaciones de este ejercicio
res <- replicate(100, {
pop$evento[pop$grupo=="e"] <- rbinom(n = 3E5, size = 1, prob = 0.006)
return(100 * (mean(pop$evento) / 0.004 - 1))
})Y si dibujamos la función de densidad tenemos
plot(density(res), main = "% de mejora", lwd = 2, col = "darkblue")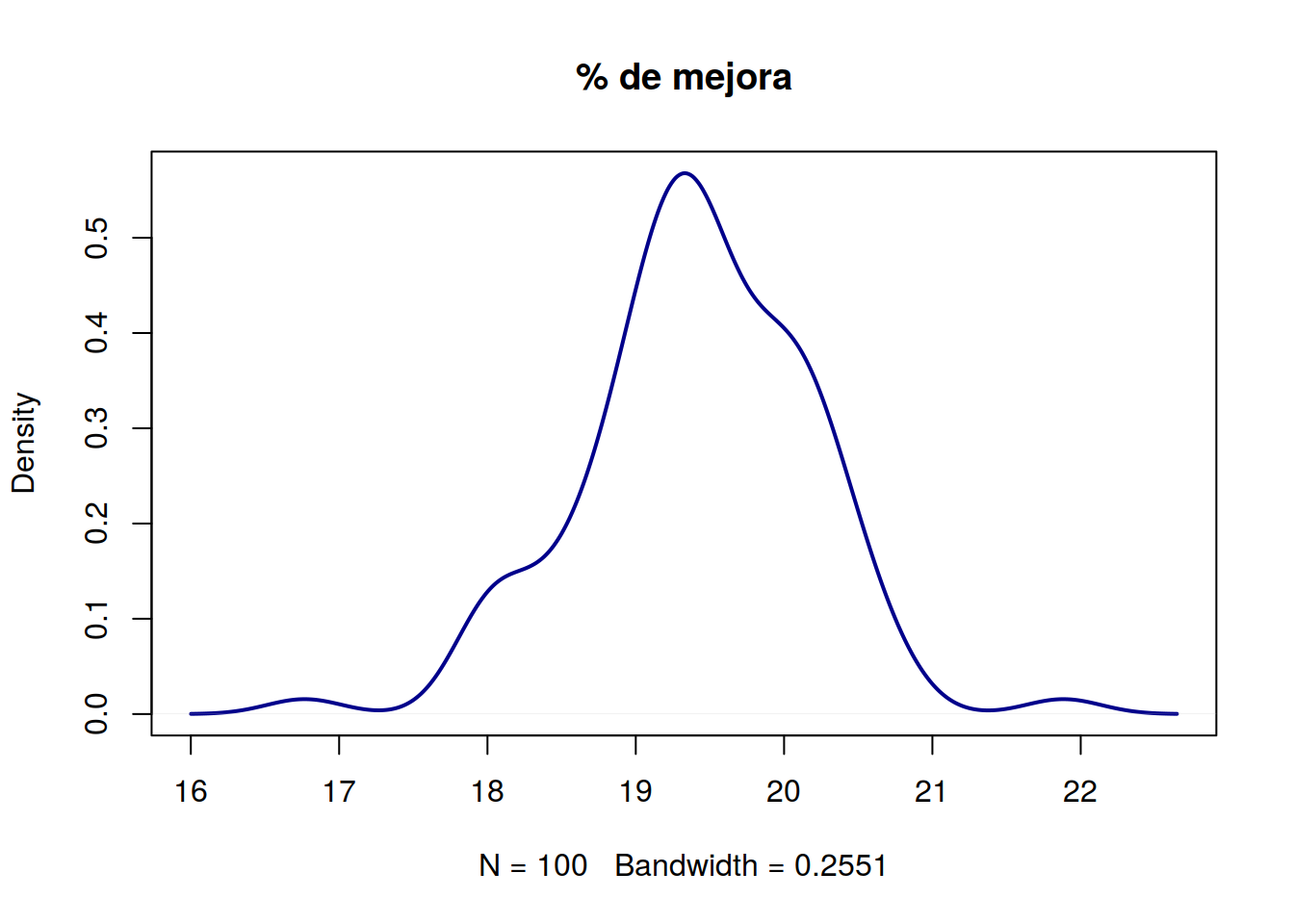
Vaya, pues parece que aún encontrando ese grupo tan molón y quitando el grupo malo mi mejora se va a quedar en torno al 19%.. Uhmm, ¿qué le digo a mi jefe cuándo me pida una mejora del 30%?
comments powered by Disqus