Hoy vamos a comparar dos formas de codificar variables categóricas basadas en reducción de dimensionalidad, a saber, embeddings con redes neuronales frente a Análisis de Correspondencias.
Para eso vamos a utilizar unos datos de kaggle de hace 2 años, se trata de un dataset donde se recoge el número de bicicletas que cruzan a diario los principales puentes de NY, datos
La idea es hacer un modelo muy simple para predecir el número de ciclistas que cruzan a diario por “Manhattan.Bridge” usando como variable explicativa el día de la semana. El día de la semana lo codificaremos de 3 formas distintas.
- Codificación parcial (One hot encoder)
- Codificación con embeddings en 3 dimensiones
- Codificación usando análisis de correspondencias con 3 dimensiones
Para la codificación con embeddings y el análisis de correspondencias utilizaremos la relación que hay entre el número de ciclistas que cruzan el puente de Brooklyn y el día de la semana.
Datos
library(tidyverse)## ── Attaching packages ──────────────────────────────── tidyverse 1.2.1 ──## ✔ ggplot2 3.1.0 ✔ purrr 0.3.2
## ✔ tibble 2.1.1 ✔ dplyr 0.8.0.1
## ✔ tidyr 0.8.3 ✔ stringr 1.4.0
## ✔ readr 1.3.1 ✔ forcats 0.4.0## ── Conflicts ─────────────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag() masks stats::lag()df <- read.csv("../../data/nyc-east-river-bicycle-counts.csv")
df <- df[,-1]
df <- df[, c("Date", "Brooklyn.Bridge", "Manhattan.Bridge")]
df <- unique(df)
df$date <- as.Date(df$Date)
df$weekday <- lubridate::wday(df$date)
DT::datatable(df)Codificación con embeddings
Creamos la variable Scaledusers como la variable estandarizada del número de ciclistas que cruzan el puente de Brooklyn
df$users <- df$Brooklyn.Bridge
df <- df[df$users > 0, ]
df <- df[!is.na(df$users), ]
df <- df[!is.na(df$weekday), ]
df$ScaledUsers <- scale(df$users)Queremos hacer un embeddings de la variable día de la semana, para eso vamos a utilizar keras
# indico que voy a usar el entorno de python y tensorflow donde tengo instalado keras
Sys.setenv(RETICULATE_PYTHON = "/home/jose/.virtualenvs/r-tensorflow/bin/python")
library(keras)
# capa de entrada
inp1 <- layer_input(shape = c(1), name = 'inp_weekday')
# capa de embeding donde reducimos a dimensión 3
embedding_out1 <-
inp1 %>% layer_embedding(
input_dim = 7 + 1, # 7 dias mas bias
output_dim = 3, # queremos 3 dimensiones embedding
input_length = 1,
name = "embedding_weekday"
) %>% layer_flatten()
# inicio modelo combinado
modelo_combinado <- keras_model_sequential()
# arquitectura:
# capa de embedding + una capa densa de 20 neuronas
modelo_combinado <- embedding_out1 %>%
layer_dense(units = 20, activation = "relu") %>%
layer_dense(units = 1)
# juntamos capa de entrada más las capas que tienen el embedding, y las densas
model <- keras::keras_model(inputs = inp1, outputs = modelo_combinado)Tenenos un modelo con 125 parámetros, ¿realmente tiene sentido esto?
summary(model)## ___________________________________________________________________________
## Layer (type) Output Shape Param #
## ===========================================================================
## inp_weekday (InputLayer) (None, 1) 0
## ___________________________________________________________________________
## embedding_weekday (Embedding) (None, 1, 3) 24
## ___________________________________________________________________________
## flatten_1 (Flatten) (None, 3) 0
## ___________________________________________________________________________
## dense_1 (Dense) (None, 20) 80
## ___________________________________________________________________________
## dense_2 (Dense) (None, 1) 21
## ===========================================================================
## Total params: 125
## Trainable params: 125
## Non-trainable params: 0
## ___________________________________________________________________________model %>%
deepviz::plot_model()Compilamos el modelo, eligiendo que lo ajuste por gradiente descendente estocástico
model %>%
compile(loss = "mean_squared_error", optimizer = "sgd", metric="accuracy") Ajustamos el modelo
inputVariables <- list(as.matrix(df$weekday))
hist <- model %>%
fit(
x = inputVariables,
y = as.matrix(df$ScaledUsers),
epochs = 70,
batch_size = 2
)Extraemos la capa de embeddings, y vemos las 3 dimensiones extraídas
layer <- get_layer(model, "embedding_weekday")
embeddings_wday <- data.frame(layer$get_weights()[[1]])
embeddings_wday## X1 X2 X3
## 1 -0.043044936 -0.03500011 0.01742882
## 2 0.114643887 -0.07663260 0.21111749
## 3 -0.107565761 -0.04164825 -0.08763187
## 4 0.105061002 -0.06102847 0.20929545
## 5 -0.117075324 0.12431101 -0.38657519
## 6 -0.119295932 0.01848904 -0.10451434
## 7 -0.002129603 0.03943805 -0.02335814
## 8 0.251920283 -0.07531382 0.28962144Juntamos con el dataset original
embeddings_wday$name <- c("none", levels(lubridate::wday(df$date, label = T)))
df$weekDayF <- lubridate::wday(df$date, label = T)
embeddings_wday$lookup <- c("none", levels(df$weekDayF))
df <- df %>%
left_join( embeddings_wday, by= c("weekDayF" = "lookup"))## Warning: Column `weekDayF`/`lookup` joining factor and character vector,
## coercing into character vectordf %>%
select(weekDayF, X1, X2, X3) %>%
head()## weekDayF X1 X2 X3
## 1 Fri -0.002129603 0.03943805 -0.02335814
## 2 Sat 0.251920283 -0.07531382 0.28962144
## 3 Sun 0.114643887 -0.07663260 0.21111749
## 4 Mon -0.107565761 -0.04164825 -0.08763187
## 5 Tue 0.105061002 -0.06102847 0.20929545
## 6 Wed -0.117075324 0.12431101 -0.38657519Codificación usando análisis de correspondencias simple
En el análisis de correspondencias clásico las variables han de ser categóricas, así que categorizamos el número de ciclistas que cruzan por Brooklyn en 5 niveles.
df$brooklyn_cat <- cut(df$Brooklyn.Bridge,5)
table(df$brooklyn_cat)##
## (501,1.18e+03] (1.18e+03,1.85e+03] (1.85e+03,2.52e+03]
## 5 4 8
## (2.52e+03,3.2e+03] (3.2e+03,3.87e+03]
## 6 7Y ahora aplicamos el análisis de correspondencias entre las variables brooklyn_cat y weekDayF
Nota. Utilizo la función MCA del correspondencias múltiples porque es más sencillo extraer las dimensiones.
library(FactoMineR)
library(factoextra)## Welcome! Related Books: `Practical Guide To Cluster Analysis in R` at https://goo.gl/13EFCZres_ca <- MCA(df[, c("brooklyn_cat","weekDayF")], ncp = 3, graph = FALSE)
fviz_mca(res_ca)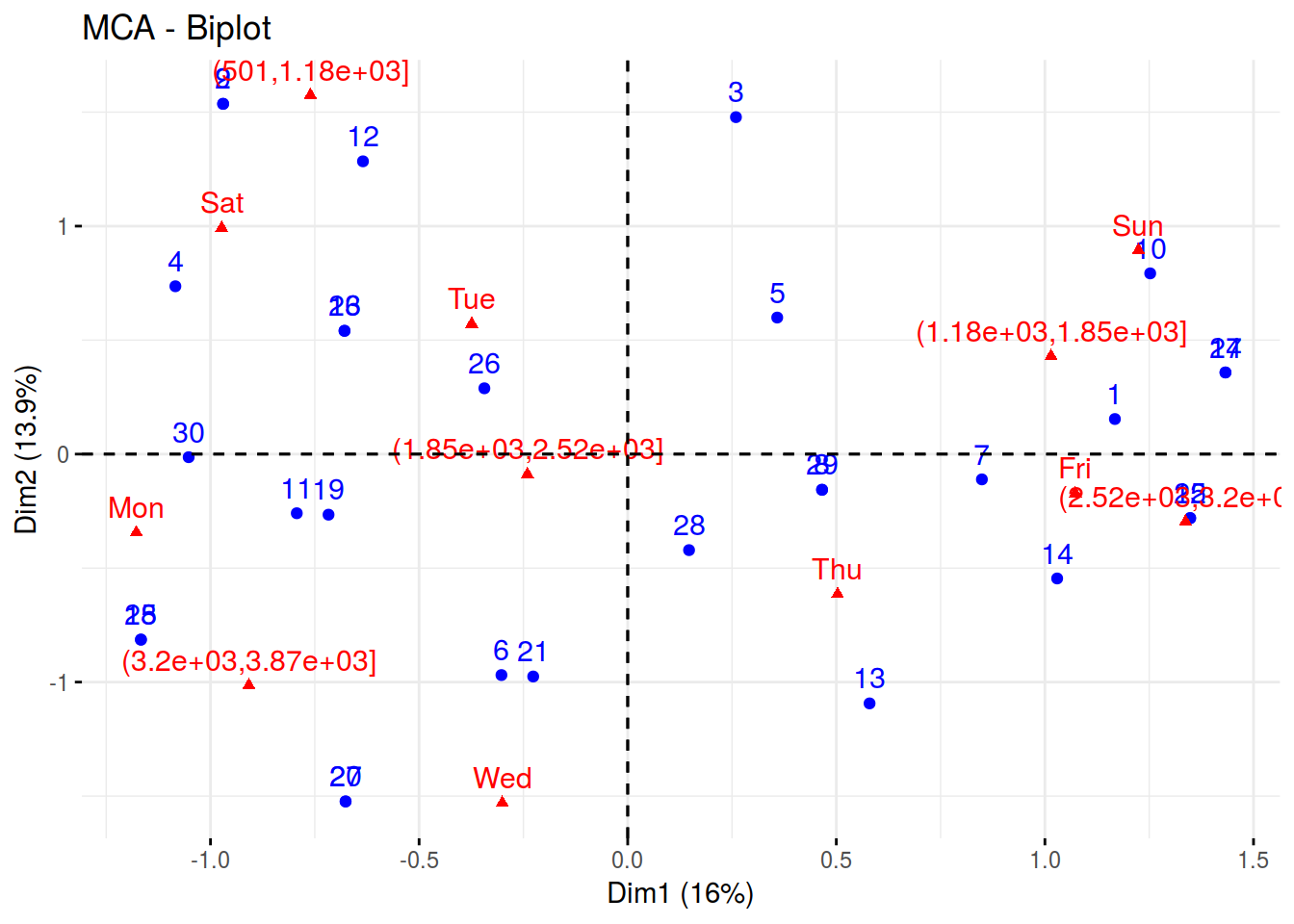
Extraigo las dimensiones
coordenadas <- as.data.frame(res_ca$ind$coord)
colnames(coordenadas) <- paste0("MCA_",1:3)
df <- cbind(df, coordenadas)
df %>%
select_at(c(paste0("MCA_",1:3), paste0("X",1:3))) %>%
DT::datatable(.)Veamos si están correlacionadas ambas codificaciones.
correlaciones <- cor(df[,c(paste0("X",1:3),paste0("MCA_",1:3))])
round(correlaciones, 2)## X1 X2 X3 MCA_1 MCA_2 MCA_3
## X1 1.00 -0.71 0.90 -0.10 0.75 -0.12
## X2 -0.71 1.00 -0.91 0.18 -0.76 -0.16
## X3 0.90 -0.91 1.00 -0.02 0.83 -0.05
## MCA_1 -0.10 0.18 -0.02 1.00 0.00 0.00
## MCA_2 0.75 -0.76 0.83 0.00 1.00 0.00
## MCA_3 -0.12 -0.16 -0.05 0.00 0.00 1.00Modelos
Una vez que ya tenemos las dos codificaciones utilizando la relación entre el número de ciclistas que cruzan por el puente de Brooklyn y los días de la semana, veamos si alguna de esas codificaciones es útil a la hora de predecir el número de ciclistas que cruzan por el puente de Manhattan.
Creamos función que ajuste unos modelos lineales simples, utilizando la codificación usual, la obtenida por Embedding y la obtenida por análisis de correspondencias.
testRun <- function(x) {
sample <- caret::createDataPartition(df$weekDayF, list = FALSE, p = 0.8)
train <- df[sample,]
test <- df[-sample,]
fit1 <- lm(Manhattan.Bridge ~ weekDayF, data = train)
fit2 <- lm(Manhattan.Bridge ~ X1 + X2 + X3, data = train)
fit3 <- lm(Manhattan.Bridge ~ MCA_1 + MCA_2 + MCA_3, data = train)
data.frame(
run = x,
Categ = sqrt(mean((predict(fit1, test) - test$Manhattan.Bridge) ^ 2)),
Embedding = sqrt(mean((predict(fit2, test) - test$Manhattan.Bridge) ^ 2)),
Corresp = sqrt(mean((predict(fit3, test) - test$Manhattan.Bridge) ^ 2))
)
}Aplicamos el proceso 200 veces y pintamos los rmse obtenidos
test <- map_df(1:200, testRun)
mm <- gather(test, key = "Tipo_codificacion", value = "rmse", -run )
ggplot(mm, aes(x=Tipo_codificacion, y= rmse)) +
geom_boxplot()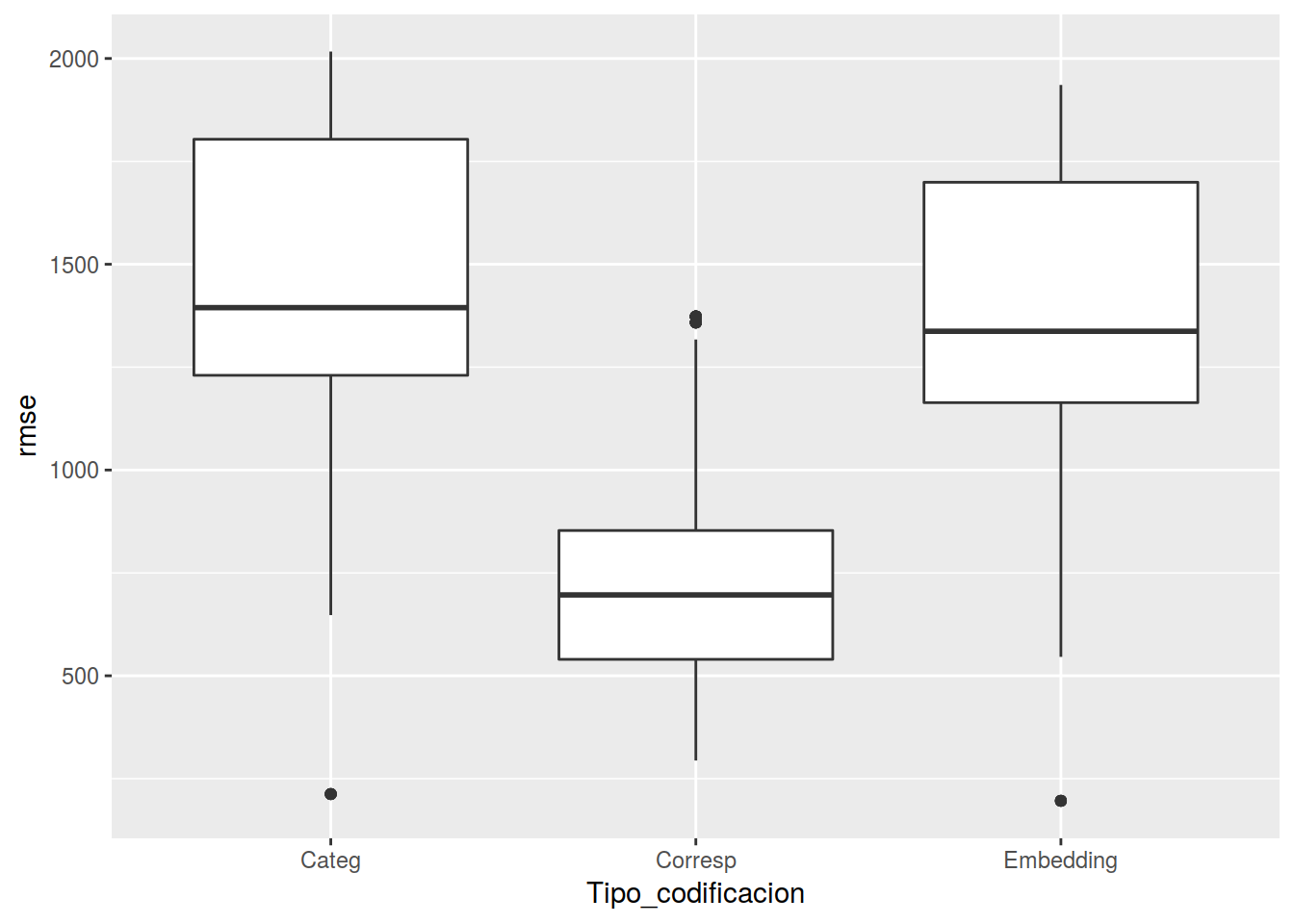
Y parece, que al menos en este caso se imponen las técnicas clásicas sobre el “Deep Learning”