Ya estuve hablando algo del partial pooling y existe un caso en el que es particularmente útil, se trata de cuando tenemos que estimar en áreas pequeñas. Entendamos áreas pequeñas cuando tenemos pocos datos en alguna o algunas categorías de una variable categórica.
Continuando con el ejemplo de la anterior entrada, veamos qué sucede con las estimaciones de la tasa de paro en cada provincia y cómo nos pueden ayudar los modelos mixtos.
Leemos los datos
library(MicroDatosEs)
library(tidyverse)
library(lme4)
fpath <- "~/Dropbox/Public/datos_4t18/md_EPA_2018T4.txt"
epa <- epa2005(fpath)
names(epa) <- tolower(names(epa))
epa <- epa[, c("prov", "edad", "nforma", "aoi")]Recodificamos
recodificacion <- function(dat) {
dat$aoi[grepl("^Inactivos", dat$aoi)] <- "i"
dat$aoi[grepl("[O-o]cupados", dat$aoi)] <- "o"
dat$aoi[grepl("^Parados", dat$aoi)] <- "p"
dat$aoi <- factor(dat$aoi)
dat$gedad <- dat$edad
dat$gedad[dat$edad == "de 0 A 4 años" |
dat$edad == "de 5 A 9 años" |
dat$edad == "de 10 A 15 años"] <- "15 años o menos "
dat$gedad[dat$edad == "de 16 A 19 años" |
dat$edad == "de 20 A 24 años" |
dat$edad == "de 25 A 29 años" |
dat$edad == "de 30 A 34 años"] <- "De 16 a 34"
dat$gedad[dat$edad == "de 35 A 39 años" |
dat$edad == "de 40 A 44 años" |
dat$edad == "de 45 A 49 años" |
dat$edad == "de 50 A 54 años"] <- "De 35 a 54"
dat$gedad[dat$edad == "de 55 A 59 años" |
dat$edad == "de 60 A 64 años" |
dat$edad == "65 o más años"] <- "55 o más"
dat$gedad <-
factor(dat$gedad,
levels = c("15 años o menos ", "De 16 a 34", "De 35 a 54", "55 o más"))
dat
}
epa <- recodificacion(epa)Quitamos menores de 15 años e inactivos
# eliminar menores de 16 años
epa <- epa[epa$gedad != "15 años o menos ", ]
# eliminar inactivos
epa <- epa[epa$aoi != "i", ]
epa <- epa[, c("aoi","gedad","prov")]
# quitamos niveles sobrantes y convetimos provincia en tipo factor
epa$gedad <- droplevels(epa$gedad)
epa$prov <- factor(epa$prov)
# calculamos número de filas en cada provincia
epa <- epa %>%
group_by(prov) %>%
mutate(tam = n()) %>%
ungroup
epa$prov <- reorder(epa$prov, epa$tam)
head(epa)## # A tibble: 6 x 4
## aoi gedad prov tam
## <fct> <fct> <fct> <int>
## 1 o De 35 a 54 Álava 722
## 2 o De 35 a 54 Álava 722
## 3 o De 35 a 54 Álava 722
## 4 o De 35 a 54 Álava 722
## 5 o De 35 a 54 Álava 722
## 6 o De 35 a 54 Álava 722Estimaciones usando muestreo y modelos mixtos
Dividimos los datos en 2. Una parte para tener una estimación de “referencia” y otra para muestrear y ver si se parece o no a la estimación de referencia.
epa$id <- seq_len(nrow(epa))
# Muestreo estratificando por provincia y grupo de edad
muestra_base <- epa %>%
group_by(prov, gedad) %>%
sample_frac(0.5) %>%
ungroup
epa_remain <- epa %>% anti_join(muestra_base, by = "id") La estimación que tomaremos como referencia será
estim_tparo <- muestra_base %>%
group_by(prov, gedad) %>%
summarise(tparo = mean(aoi == "p", na.rm = TRUE),
tam = first(tam)) %>%
ungroup
DT::datatable(estim_tparo)Construimos data.frame con todas las combinaciones de provincia y grupo de edad que será nuestro data.frame a predecir por el modelo mixto
dat_ficti <- expand.grid(prov = levels(epa$prov), gedad = levels(epa$gedad))
head(dat_ficti)## prov gedad
## 1 Ceuta De 16 a 34
## 2 Melilla De 16 a 34
## 3 Soria De 16 a 34
## 4 Huelva De 16 a 34
## 5 Palencia De 16 a 34
## 6 Zamora De 16 a 34Creamos función para estimar según un modelo mixto y calculamos el error con respecto a las estimaciones base y también comparamos con las estimaciones directas y con un modelo logit clásico que tenga los efectos principales de provincia y edad.
Nótese que las estimaciones directas coinciden con las estimaciones usando un modelo logit clásico que tenga los efectos principales y la interacción entre provincia y edad.
Estimar_tparo <- function(muestra, dat_ficti,...) {
modelo_glmer <- glmer(aoi == "p" ~ (1 |prov) + (1 | gedad),
data = muestra,
family = binomial)
modelo_clasico <- glm(aoi == "p" ~ prov + gedad,
data = muestra,
family = binomial )
# con modelos mixtos se pueden estimar hasta categorías qeu no estén en la muestra
dat_ficti$tparo_glmer <- predict(modelo_glmer,
newdata = dat_ficti,
type = "response",
allow.new.levels = TRUE)
predict_glm_safely <- possibly(
function(modelo, newdata){
predict(modelo, newdata = newdata,
type = "response")},
otherwise = NA)
dat_ficti$tparo_glm <- predict_glm_safely(modelo_clasico, dat_ficti)
estim_directas <- muestra %>%
group_by(prov, gedad) %>%
summarise(tparo_directa = mean(aoi == "p", na.rm = TRUE))
res <- dat_ficti %>%
left_join(estim_tparo, by = c("prov", "gedad")) %>%
left_join(estim_directas, by = c("prov", "gedad")) %>%
mutate(
error_abs_glmer = abs(tparo - tparo_glmer),
error_abs_glm = abs(tparo - tparo_glm),
error_abs_directas = abs(tparo - tparo_directa))
res
}Creamos función para pintar los errores con respecto a la estimación de referencia. Cada punto es la estimación en una provincia e intervalo de edad por cada uno de los métodos.
plot_errores <- function(res, title, span = 1){
res_tidyr <- res %>%
select(prov, gedad, tam, error_abs_glmer, error_abs_glm, error_abs_directas) %>%
gather(tipo, error_abs, -prov , -gedad, -tam)
res_tidyr %>%
ggplot(aes(x = tam, y = error_abs, col = tipo)) +
geom_point(size = rel(0.6)) +
geom_smooth(span = span, se = FALSE) +
facet_wrap(~gedad) +
ylim(0,0.5) +
labs(x = "Individuos en cada provincia", title = title)
}Muestra del 5% que se corresponden con 1864 datos
res_1 <- Estimar_tparo(muestra = epa_remain %>% sample_frac(0.05), dat_ficti = dat_ficti)
plot_errores(res_1, "Muestra del 5%")## `geom_smooth()` using method = 'loess' and formula 'y ~ x'## Warning: Removed 2 rows containing non-finite values (stat_smooth).## Warning: Removed 2 rows containing missing values (geom_point).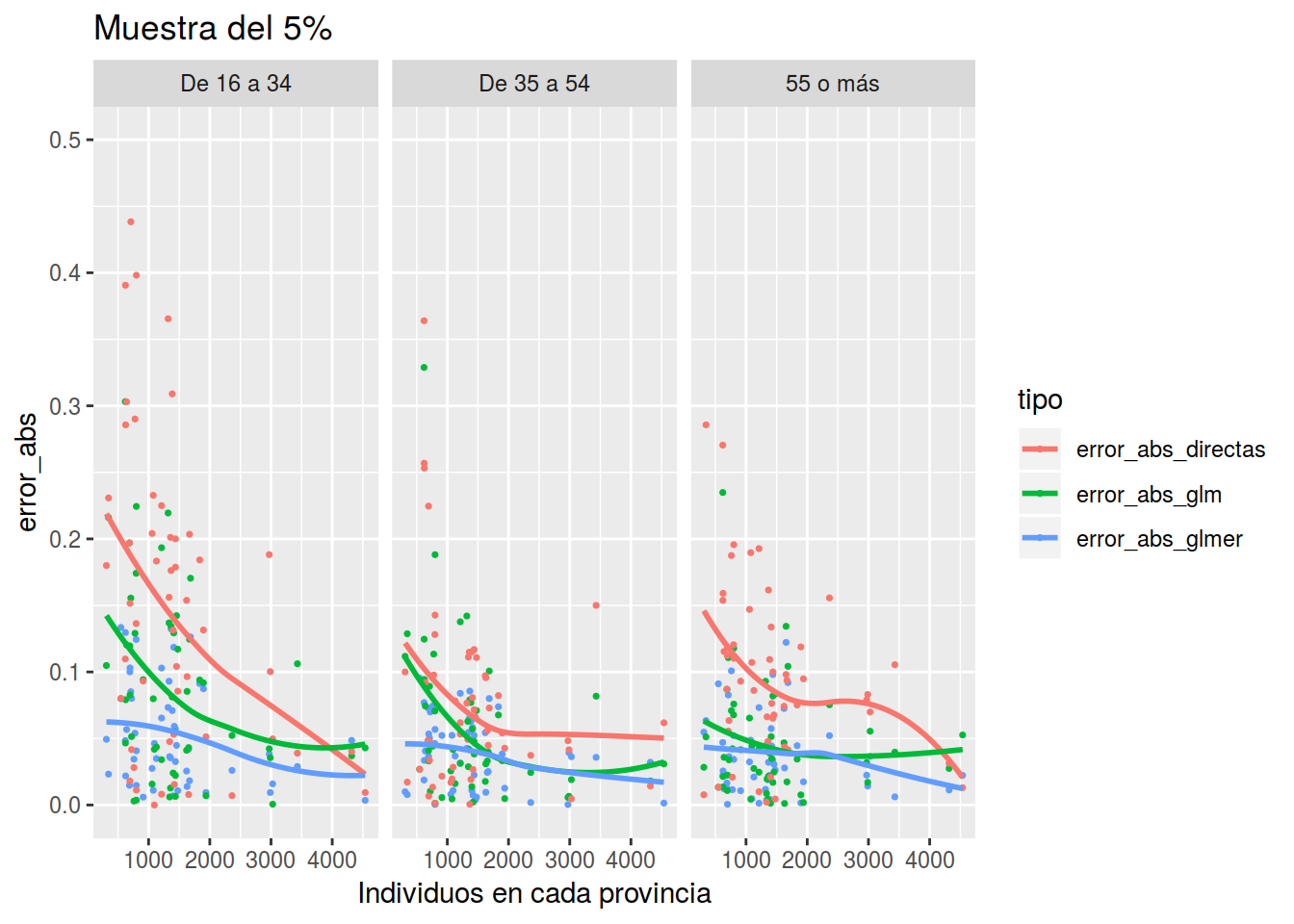
Muestras de 10% que se corresponden con 3727 datos
res_10 <- Estimar_tparo(muestra = epa_remain %>% sample_frac(0.1), dat_ficti = dat_ficti)
plot_errores(res_10, "Muestra del 10%")## `geom_smooth()` using method = 'loess' and formula 'y ~ x'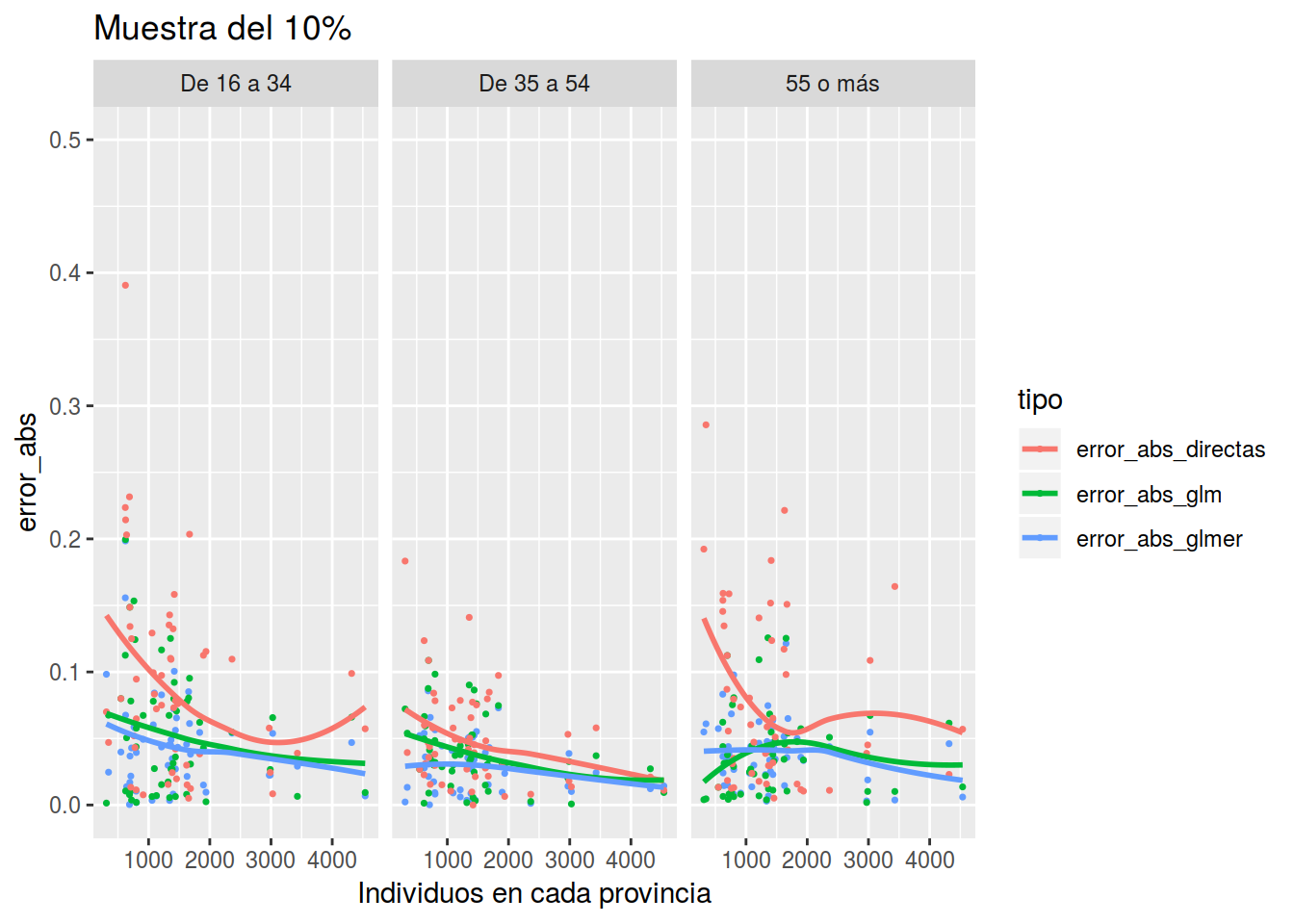
Muestras de 50% que se corresponden con 1.863610^{4} datos
res_50 <- Estimar_tparo(muestra = epa_remain %>% sample_frac(0.5), dat_ficti = dat_ficti)
plot_errores(res_50, "Muestra del 50%")## `geom_smooth()` using method = 'loess' and formula 'y ~ x'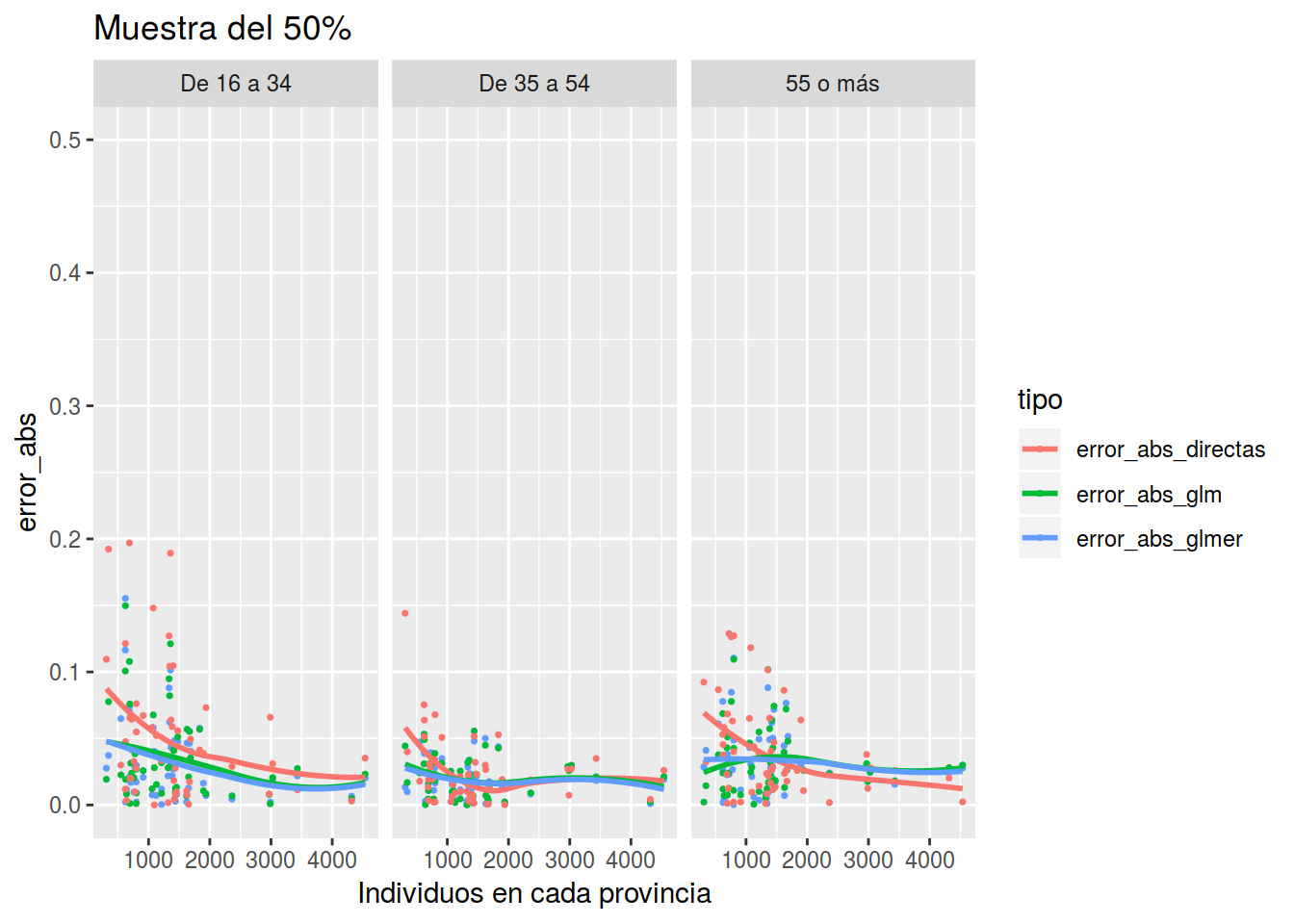
Y vemos que con poco tamaño muestral, el modelo con glmer es mucho mejor y conforme aumenta el tamaño muestral se van igualando. Cómo decía un lector del blog “de dónde no hay no se puede sacar”, pero hagamos lo posible por sacar algo.