Muestreando · Muestrear no es pecado

10 Feb 2019

estadística / muestreo

Vamos con el post. El INE tiene un ftp no muy publicitado aquí, yo suelo descargarme la Encuesta de Población Activa de este sitio, hay un fichero comprimido que tiene varias carpetas dónde hay script para poder importar los datos con Stata, SAS, spss y R. Gracias INE!!.

El caso es que es que yo para la epa uso el paquete MicroDatosEs de Carlos Gil Bellosta

Leo la EPA y me quedo sólo con la provincia, edad y aoi (que indica si una persona es inactiva, si está ocupada, parada, etc ). El factor de elevación lo he obviado, por si alguien lo echa de menos.

library(MicroDatosEs)

FALSE Loading required package: readr

fpath <- "~/Dropbox/Public/datos_4t18/md_EPA_2018T4.txt"

epa <- epa2005(fpath)
names(epa) <- tolower(names(epa))
epa <- epa[,c("prov", "edad", "aoi")]

Recodifico la variable aoi y quito los inactivos y los menores de 16 años (la sintaxis “viejuna” es intencionada)

epa <-  subset(epa, edad != "de 0 A 4 años" & edad != "de 5 A 9 años" & edad != "de 10 A 15 años" )
  
epa$aoi[grepl("^Inactivos", epa$aoi)] <- "i"
epa$aoi[grepl("[O-o]cupados", epa$aoi)] <- "o"
epa$aoi[grepl("^Parados", epa$aoi)] <- "p"

epa$aoi <- factor(epa$aoi)

El número de filas en la epa una vez quitados los inactivos es de 137992. Si consideramos como nuestra población estos datos la tasa de paro sería.

round(100 *mean(epa$aoi=="p"), 3)

## [1] 7.748

¿Qué pasa si muestreamos de forma aleatoria (muestreo con reemplazamiento),y nos quedamos con 2000 filas, por ejemplo?

set.seed(43)
idx <- sample(1:nrow(epa), size = 2000, replace = TRUE)
round(100 * mean(epa$aoi[idx] == "p"), 2)

## [1] 7.1

Pues parece que tal y como nos enseñaron tampoco nos alejamos tanto. ¿Y si repetimos el proceso 10000 veces?

Calcular_tasa <- function(){
  idx <- sample(1:nrow(epa), size = 2000, replace = TRUE)
  round(100 * mean(epa$aoi[idx] == "p"), 2)
  
}
tasas <- replicate(10000, Calcular_tasa() )

hist(tasas, breaks= 30, col = "darkorange")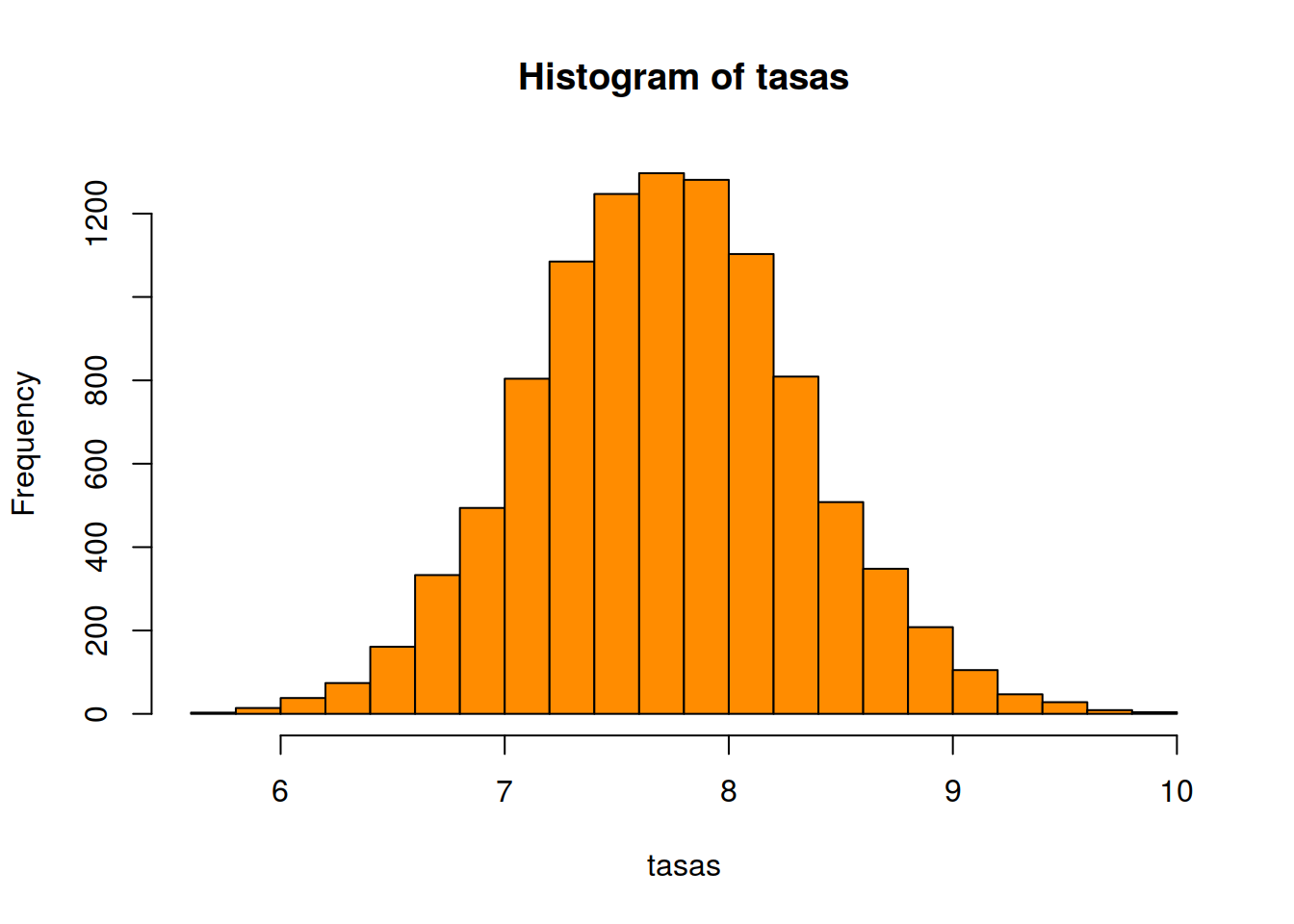

Y la mediana y el rango del 95% de los valores centrales

median(tasas)

## [1] 7.75

quantile(tasas, probs = c(0.025, 0.975))

##  2.5% 97.5% 
##  6.60  8.95

Así que para calcular un valor poblacional parece que el muestreo funciona (cómo ya sabíamos desde hace años). En próximas entradas veremos como si bajamos la granularidad y queremos estimar en un dominio más pequeño tendremos más problemas, y cómo los modelos mixtos nos pueden ayudar.

Así que ya saben, muestrear no es pecado , a pesar de lo que digan los adalides del big data.