Volviendo al tema de los modelos mixtos, hay una particularidad que me gusta bastante y es la posibilidad de incluir predictores a nivel de grupo. Imaginemos que queremos estimar algo a nivel provincial, por ejemplo el salario medio. Para eso hemos preguntado de forma aleatoria (entendemos que con un muestreo bien hecho, tipo estratificado por provincias o similar) y tenemos unos datos con los que estimar. Supongamos que para cada encuestado tenemos su salario, su edad y la provincia a la que pertenece.
En un modelo lineal clásico tendríamos 53 coeficientes
\(y_i \sim \mathcal{N}(\beta_0 + \beta_1 \cdot edad_i + \beta_2 \cdot prov_2 + \ldots + \beta_{52} \cdot prov_{52},\; \sigma^2)\)
Dónde \(\beta_0\) sería el coeficiente para la categoría de referencia de la variable provincia para edad=0.
Supongamos también que tenemos el número de empresas de más de 50 empleados en cada provincia y queremos meter esa variable en el modelo. El problema es que para todos los encuestados de la misma provincia tenemos el mismo valor del número de empresas con lo que en un modelo de regresión lineal clásico tenemos colinealidad perfecta y se devuelven NA’s para los coeficientes sobrantes.
Sin embargo, en un modelo mixto se pueden incluir variables a nivel de las variables categóricas sin problema, es lo que conoce como los “group level predictors”. Gelman comenta lo siguiente “Los group-level predictors juegan un papel importante en los modelos multinivel ya que reducen la variabilidad no explicada a nivel de grupo”.
Los group-level predictors hace que se incremente la cantidad de información compartida y se consiguen \(\alpha_j\) más precisos, especialmente en los grupos con menor muestra.
Nuestro modelo quedaría algo así como
\(y_i \sim \mathcal{N}(\beta_o + \beta_1 \cdot edad + \alpha_j \cdot provincia , \; \sigma^2_{y})\)
dónde
\(\alpha_j \sim \mathcal{N}(\gamma_1 \cdot \text{empresas}_j , \;\sigma^{2}_{prov} ) \; j = 1 \ldots 52\)
Despúes de todo este rollo y cómo no me apetece nada ponerme a buscar una encuesta de salarios a nivel provincial y datos del número de empresas en cada provincia, voy a poner unos datos simulados para ilustrar el problema de la colinealidad que induce tener variables a nivel de grupo en un modelo lineal de toda la vida.
set.seed(42)
x <- rnorm(100,3,1)
y <- 20 + 2*x + rnorm(length(x),2,0.5)
plot(x,y, pch = 19, cex = 0.7)
Modifico un poco la y para tener 3 grupos según tramos en x y me creo una variable de tipo factor que indique qué grupo es cada uno
y[x <= 2] <- y[x <= 2] - 3
y[x > 2 & x < 4] <- y[x > 2 & x < 4] + 7
y[x >= 4] <- y[x >= 4] + 13
A <- factor(c(1,2,3))
A[x<=2] <- 1
A[x>2 & x<4] <- 2
A[x>=4] <- 3
plot(x,y,col=A, pch = 19, cex = 0.7)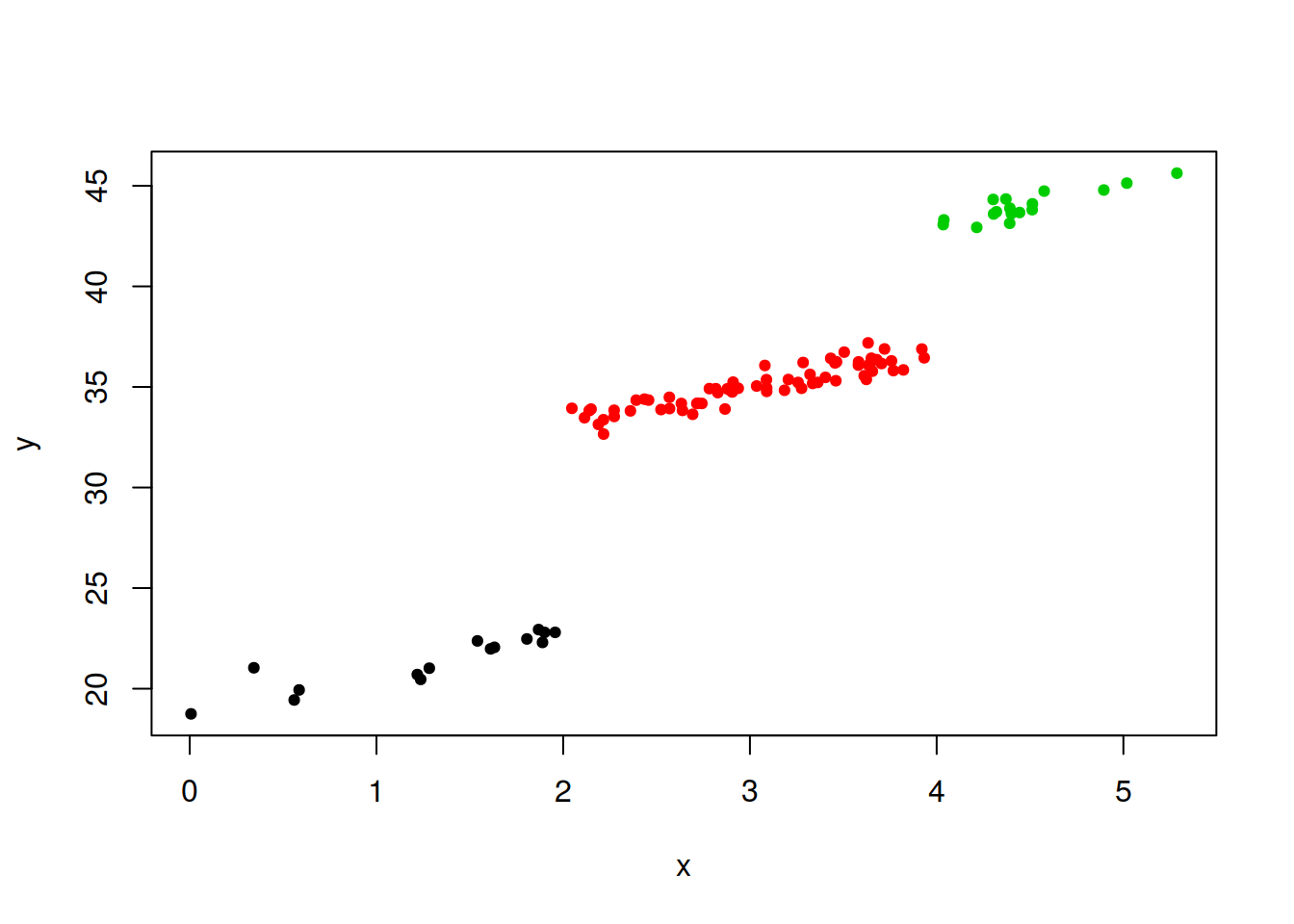
Creo variable a nivel de grupo que tenga los mismos valores para cada grupo
aux <- c(10, 20, 70 )
Z <- aux[A]
Z## [1] 70 20 20 20 20 20 70 20 70 20 70 70 10 20 20 20 20 10 10 70 20 10 20
## [24] 70 70 20 20 10 20 20 20 20 70 20 20 10 20 20 10 20 20 20 20 20 10 20
## [47] 20 70 20 20 20 20 70 20 20 20 20 20 10 20 20 20 20 70 20 70 20 70 20
## [70] 20 10 20 20 20 20 20 20 20 20 10 70 20 20 20 10 20 20 20 20 20 70 20
## [93] 20 70 10 20 10 10 20 20plot(Z,y,col=A,pch=19)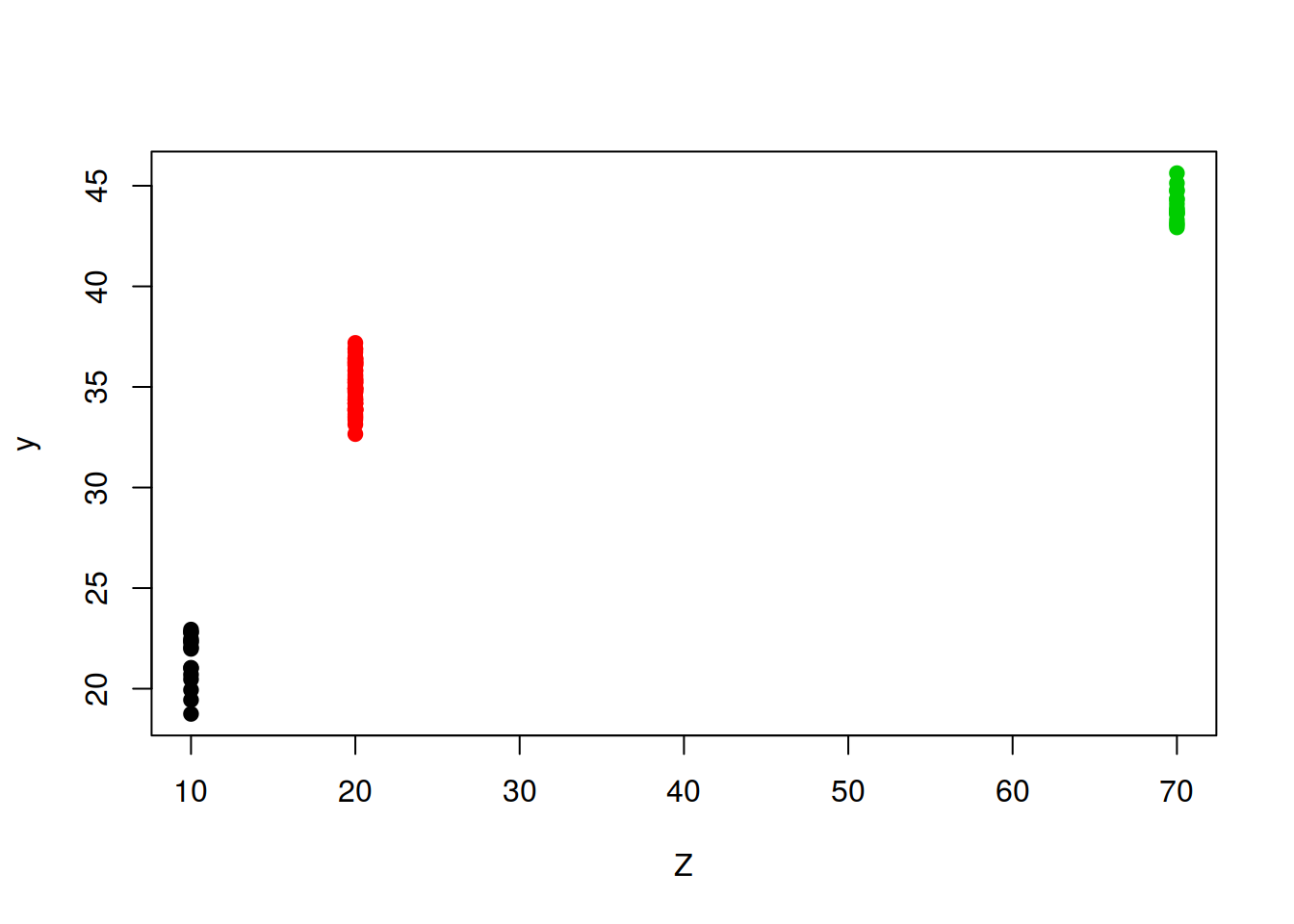
plot(x,Z, col = A, pch = 19)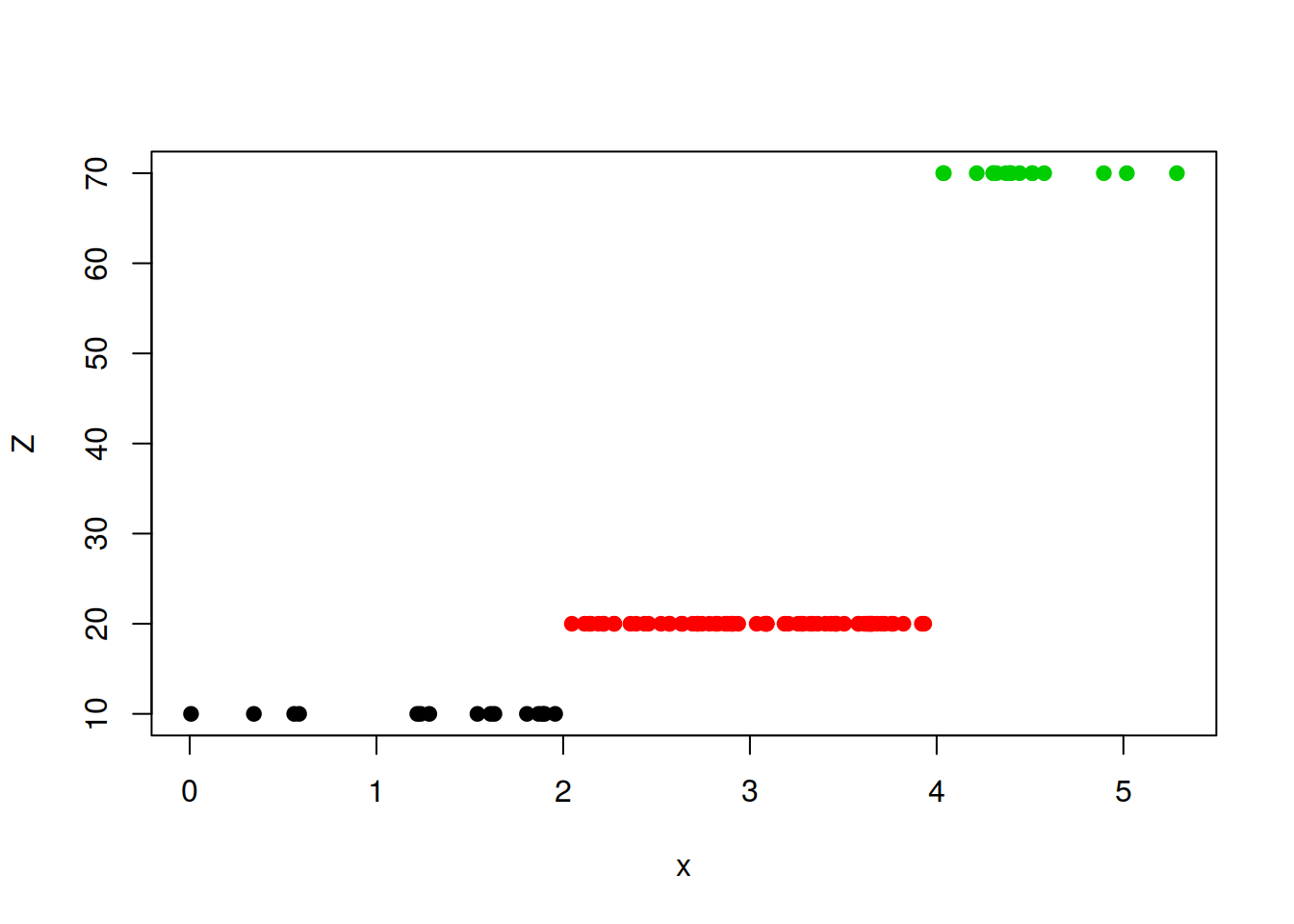
datos <- data.frame(y,x,A,Z)
DT::datatable(datos)Intentamos hacer un modelo lineal
mod1 <- lm(y ~ x + A + Z , data = datos)
summary(mod1)##
## Call:
## lm(formula = y ~ x + A + Z, data = datos)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.88145 -0.27508 0.00622 0.26219 1.38055
##
## Coefficients: (1 not defined because of singularities)
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 19.02752 0.16003 118.90 <2e-16 ***
## x 1.83370 0.08589 21.35 <2e-16 ***
## A2 10.44670 0.19746 52.91 <2e-16 ***
## A3 16.76045 0.31508 53.19 <2e-16 ***
## Z NA NA NA NA
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4453 on 96 degrees of freedom
## Multiple R-squared: 0.9955, Adjusted R-squared: 0.9954
## F-statistic: 7085 on 3 and 96 DF, p-value: < 2.2e-16Y vemos que no puede calcular el coeficiente para Z, es decir, en el modelo o metemos la variable A o la variable Z, pero no podemos meter las 2 a la vez
Veamos con un modelo multinivel, dónde metemos la variable A como efecto aleatorio y las variables x y Z como efectos fijos.
library(lme4)## Loading required package: Matrixmod_lmer <- lmer(y ~ x + Z + (1 | A), data = datos)
summary(mod_lmer)## Linear mixed model fit by REML ['lmerMod']
## Formula: y ~ x + Z + (1 | A)
## Data: datos
##
## REML criterion at convergence: 145.3
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -1.97617 -0.61594 0.01578 0.58856 3.09928
##
## Random effects:
## Groups Name Variance Std.Dev.
## A (Intercept) 33.9963 5.8306
## Residual 0.1983 0.4453
## Number of obs: 100, groups: A, 3
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 20.43012 5.44365 3.753
## x 1.83489 0.08588 21.365
## Z 0.22990 0.12834 1.791
##
## Correlation of Fixed Effects:
## (Intr) x
## x -0.023
## Z -0.784 -0.030Este modelo ha podido calcular el coeficiente de Z. Extraemos los efectos fijos, los aleatorios y todos juntos
fixef(mod_lmer)## (Intercept) x Z
## 20.4301161 1.8348901 0.2299022Efectos aleatorios
ranef(mod_lmer)## $A
## (Intercept)
## 1 -3.7017116
## 2 4.4420539
## 3 -0.7403423
##
## with conditional variances for "A"coef(mod_lmer)## $A
## (Intercept) x Z
## 1 16.72840 1.83489 0.2299022
## 2 24.87217 1.83489 0.2299022
## 3 19.68977 1.83489 0.2299022
##
## attr(,"class")
## [1] "coef.mer"Podemos dibujar los coeficientes estimados y su intervalo de confianza
sjPlot::plot_model(mod_lmer, type = "est")## Warning in checkMatrixPackageVersion(): Package version inconsistency detected.
## TMB was built with Matrix version 1.2.15
## Current Matrix version is 1.2.16
## Please re-install 'TMB' from source using install.packages('TMB', type = 'source') or ask CRAN for a binary version of 'TMB' matching CRAN's 'Matrix' package## Computing p-values via Wald-statistics approximation (treating t as Wald z).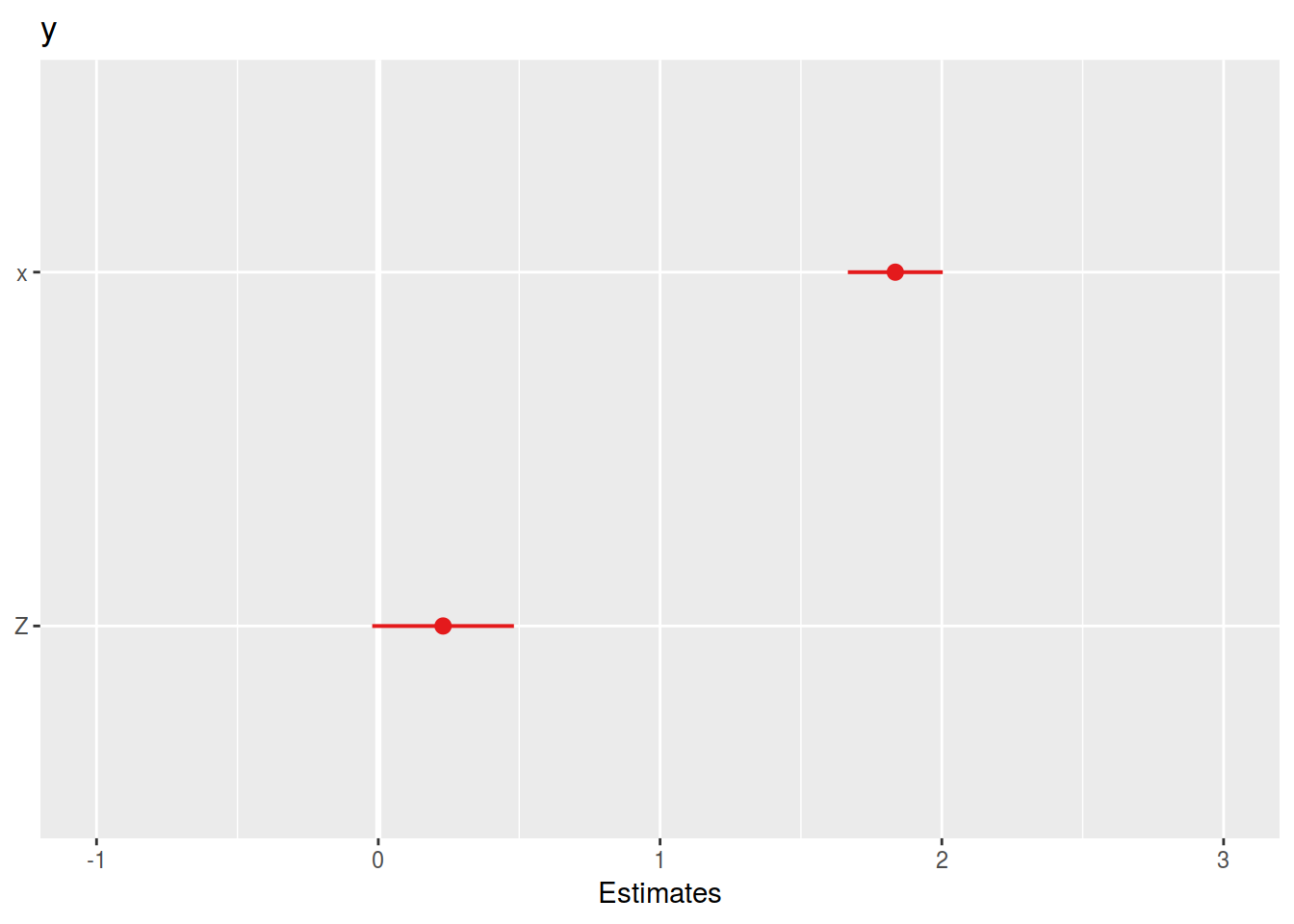
Y los efectos aleatorios serían
sjPlot::plot_model(mod_lmer, type = "re")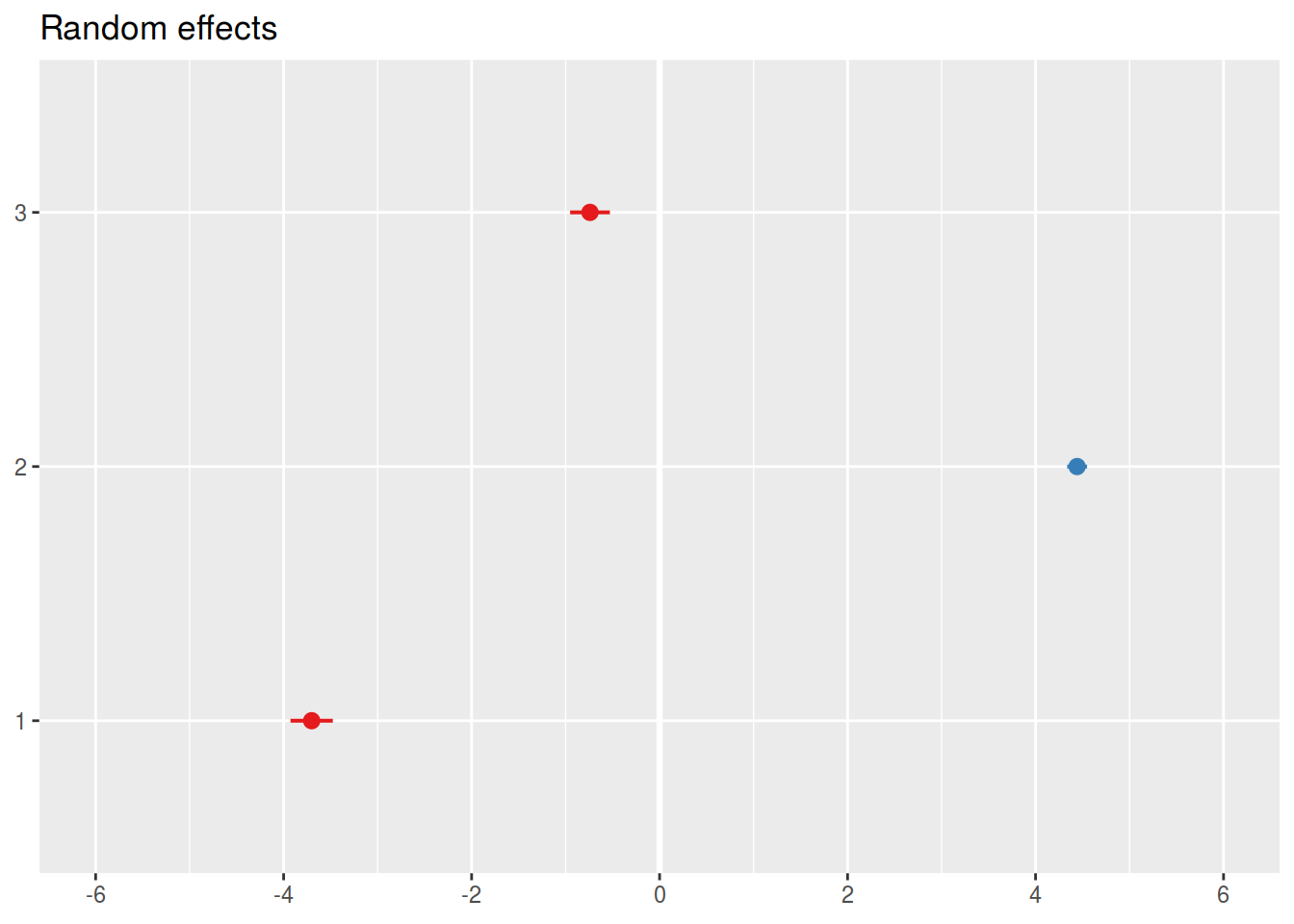
De esta forma podemos estimar efectos de variables a diferentes niveles de agregación de nuestros datos e incluir información auxiliar relevante.
comments powered by Disqus