Voy a empezar una serie de entradas (no sé cuántas) sobre modelos mixtos, una de las cosas más chulas que hay en esto de la estadística. Yo ví la luz con el libro de uno de mis ídolos Andrew Gelman. El libro en cuestión se llama Data Analysis Using Regression and Multilevel/Hierarchical Models y recomiendo su lectura encarecidamente.
Para ejemplificar de qué va esto de los modelos mixtos vamos a ver un ejemplo del libro de Gelman. Se trata de estimar el efecto del tipo de suelo y del condado sobre la concentración de radon (más concretamente sobre el logaritmo neperiano del mismo), en el estado de Minnesota.
Los datos se pueden obtener de la web del libro.
Importamos librerías
library(tidyverse)
library(lme4)srrs2 <- read_csv("/home/jose/Dropbox/Public/srrs2.dat")
# Selecciono solo los datos de Minnesota, la concentración de radon "activity", el
# tipo de suelo 0 o 1 y el condado
df_mn <- srrs2 %>%
filter(state == "MN") %>%
select(activity, floor, county) %>%
mutate(y = log(if_else(activity == 0, 0.1, activity)))
DT::datatable(df_mn)Modelo general “pooled”
Estamos interesados en estudiar el efecto del tipo de suelo sobre la concentración de radon. Si no tenemos en cuenta que hay diferentes condados, podremos estimar el modelo como y ~ floor, esto es lo que se denomina el modelo pooled
lm_pooled <- lm(y ~ floor, data = df_mn)
coef(lm_pooled)## (Intercept) floor
## 1.3267439 -0.6133948Notese que al tomar floor sólo los valores 0 y 1, los coeficiente del modelo lineal nos dan los valores medios del logaritmo de radon en los dos tipos de suelo.
with(df_mn, tapply(y, floor, mean))## 0 1
## 1.3267439 0.7133491El intercept del modelo se corresponde con la media de radon en los suelos de tipo 0 y el intercept del modelo más el coeficiente asociado a floor 1.327 - 0.613 nos da la media del logaritmo de radon en los suelos de tipo 1. Esta característica propia de los modelos lineales hacen que sean un framework más general que los t.test o los test de proporciones (si consideramos una regresión logística) y hace que estudiar los test de hipótesis casi carezca de sentido. Espero críticas de mis lectores estadísticos.
Gráficamente tendríamos esto
# pongo un poco de ruido en floor para mejorar la visualización
ggplot(df_mn, aes (x= jitter(floor, 0.1) , y = y)) +
geom_point() +
geom_smooth(method = "lm", se = FALSE) +
labs(y = "log(radon)", x = "floor")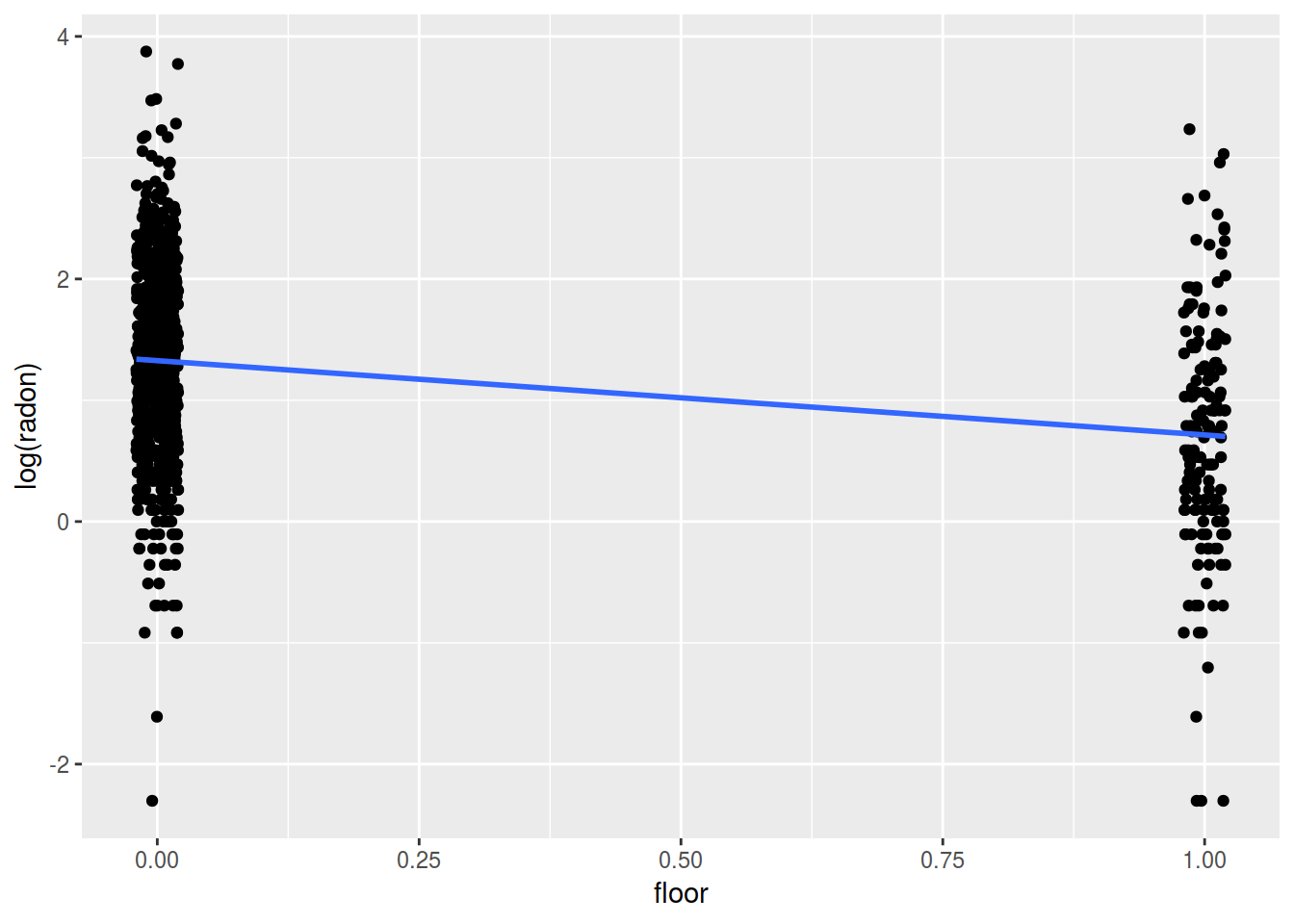
Modelo teniendo en cuenta los condados “no pooled”
Podríamos pensar que la concentración de radon no sólo se ve afectada por el tipo de suelo, sino también por el condado dónde hemos tomado las mediciones. Un posible modelo sería considerar una regresión independiente en cada condado, esto sería un modelo no pooled, otro posible modelo no pooled sería considerar que el efecto del suelo es el mismo para todos los condados pero que el hacer mediciones en un condado o en otro tiene un efecto que modifica la media del logaritmo de radon.
Hagamóslo
# pongo 0 para tener un coeficiente de cada condado en vez de tener uno que sea la categoría de referencia y su efecto esté dentro del intercept
lm_unpooled <- lm(y ~ 0 + floor + county, data = df_mn)Veamos algunos coeficientes
coef(lm_unpooled)[1:7]## floor countyAITKIN countyANOKA countyBECKER
## -0.7205390 0.8405411 0.8748191 1.5286973
## countyBELTRAMI countyBENTON countyBIG STONE
## 1.5527222 1.4325705 1.5130101Comparemos los ajustes de ambos modelos de manera gráfica, para eso nos construimos unos data.frames con los coeficientes de ambos modelos y los unimos a los atos
coef_pooled <- data.frame(
county = unique(df_mn$county),
intercept = coef(lm_pooled)[1],
coef = coef(lm_pooled)[-1],
modelo = "pooled"
)
coef_unpoled <- data.frame(
county = unique(df_mn$county),
intercept = coef(lm_unpooled)[-1],
coef = coef(lm_unpooled)[1],
modelo = "unpooled"
)
df_models <-
rbind(coef_pooled, coef_unpoled) %>% left_join(df_mn, by = "county")
DT::datatable(df_models)Y si pintamos los mismos 8 condados que ejemplifica Gelman en el libro
condados_num <- c(36, 1, 35, 21, 14, 71, 61, 70)
p_model_comparison <- df_models %>%
filter(county %in% unique(county)[condados_num]) %>%
ggplot(aes(x = jitter(floor, factor = 0.1), y = y)) +
geom_point(size = rel(0.7)) +
geom_abline(aes(intercept = intercept, slope = coef, color = modelo)) +
facet_wrap(~county) +
labs(y = "log(radon)", x = "floor")
p_model_comparison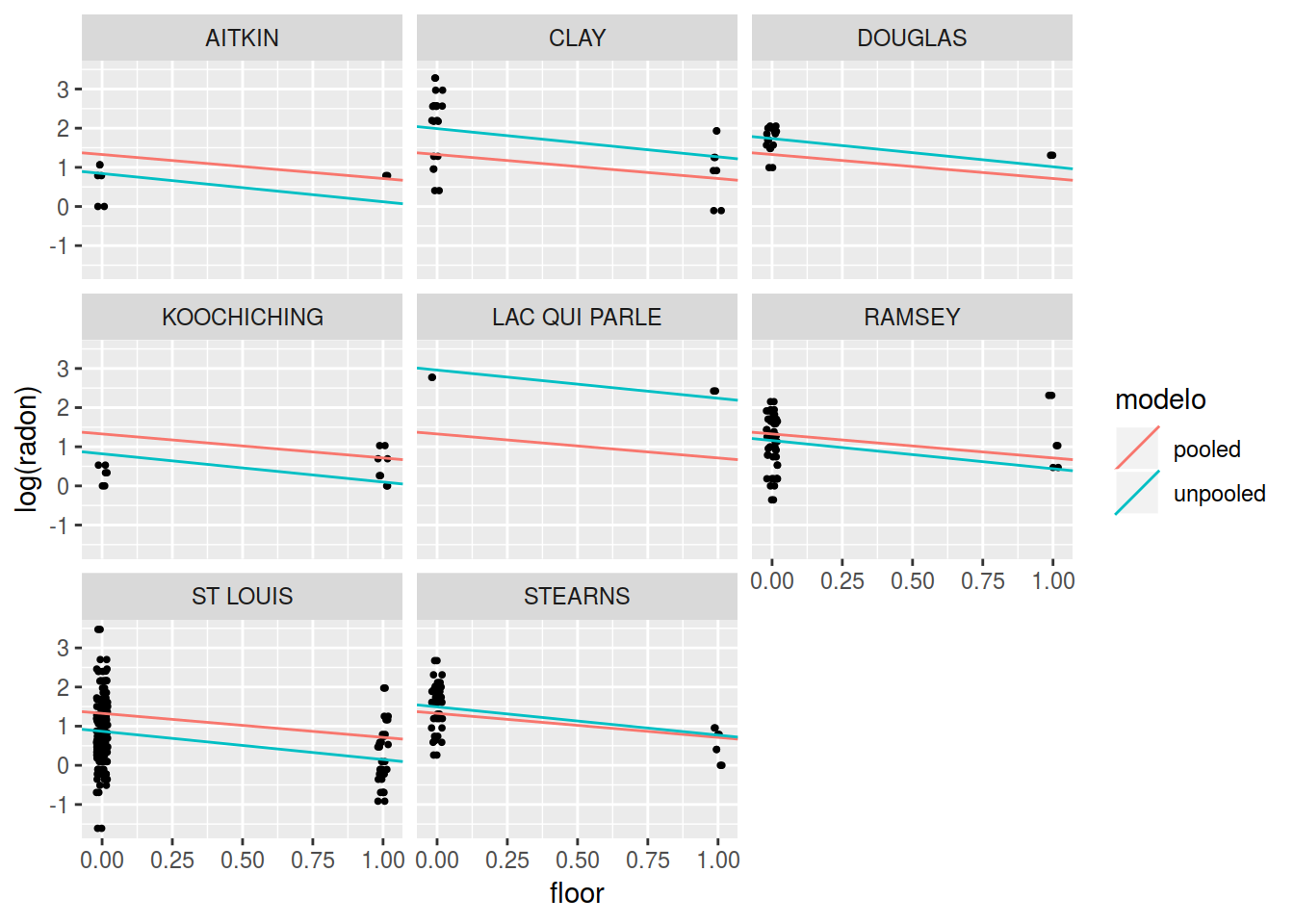
Vemos un efecto curioso, por ejemplo en el condado LAC QUI PARLE que sólo tiene 3 medidas ambos modelos son muy distintos mientras en otros condados el ajuse de ambos modelos es similar. Ambos modelos tienen problemas, si nos quedamos con el modelo pooled no tenemos en cuenta la particularidad en cada condado y si nos quedamos con el modelo no pooled la estimación en condados con pocas medidas no resulta creíble.
Modelo mixto “partial pooled”
Estos problemas se pueden resolver utilizando modelos mixtos (no voy a entrar en el detalle matemático) en dónde se realiza partial pooling de forma que, en nuestro ejemplo, para los condados con mayor número de observaciones se tiene más en cuenta la información de ese condado mientra que para los condados con menos observaciones se tiene más en cuenta la estimación general en todos los condados
Este tipo de modelos se pueden ajustar con técnicas bayesianas, pero para este caso vamos a utilizar la librería lme4 que los ajusta por máxima verosimilitud restringida.
El modelo a ajustar sería el siguiente, dónde los efectos asociados a los condados se suponen que vienen de una distribución normal con varianza \(\sigma_2\)
\(y_i \sim \mathcal{N}(\beta_o + \beta_1 \cdot floor + \alpha_j \cdot county )\)
dónde
\(\alpha_l \sim \mathcal{N}(0, \sigma^{2}_{j} ) \; j = 1 \ldots \; \text{n_counties}\)
por lo que tenemos sólo 2 parámetros a ajustar, los diferentes \(\alpha_j\) se estiman usando el estimador BLUP Best Linear Unbiased Prediction que grosso modo es una media ponderada de la media del logaritmo de radon total y la media en cada condado
\[ \widehat{\alpha}_{j}^{county}\approx\left(\dfrac{\frac{n_{j}}{\sigma_{y}^{2}}\bar{y}_{j}+\frac{1}{\sigma_{county}^{2}}\bar{y}_{total}}{\frac{n_{j}}{\sigma_{y}^{2}}+\frac{1}{\sigma_{county}^{2}}}\right) \]
Ajustamos el modelo con la librería lme4
# consideramos
lm_partial_pooled <- lmer(y ~ floor + (1 | county), data = df_mn)Con la función coef extraemos el efecto aleatorio para cada condados y el coeficiente para floor común a todos los condados
coef(lm_partial_pooled)## $county
## (Intercept) floor
## AITKIN 1.1915004 -0.6929937
## ANOKA 0.9276468 -0.6929937
## BECKER 1.4792143 -0.6929937
## BELTRAMI 1.5045012 -0.6929937
## BENTON 1.4461503 -0.6929937
## BIG STONE 1.4801817 -0.6929937
## BLUE EARTH 1.8581255 -0.6929937
## BROWN 1.6827736 -0.6929937
## CARLTON 1.1600747 -0.6929937
## CARVER 1.5086099 -0.6929937
## CASS 1.4322449 -0.6929937
## CHIPPEWA 1.5771520 -0.6929937
## CHISAGO 1.2370518 -0.6929937
## CLAY 1.8380232 -0.6929937
## CLEARWATER 1.4024982 -0.6929937
## COOK 1.2432992 -0.6929937
## COTTONWOOD 1.3723633 -0.6929937
## CROW WING 1.2209415 -0.6929937
## DAKOTA 1.3462611 -0.6929937
## DODGE 1.5840332 -0.6929937
## DOUGLAS 1.6311136 -0.6929937
## FARIBAULT 1.0211903 -0.6929937
## FILLMORE 1.4409443 -0.6929937
## FREEBORN 1.8605721 -0.6929937
## GOODHUE 1.8135585 -0.6929937
## HENNEPIN 1.3626875 -0.6929937
## HOUSTON 1.6222663 -0.6929937
## HUBBARD 1.3467692 -0.6929937
## ISANTI 1.3149879 -0.6929937
## ITASCA 1.0999775 -0.6929937
## JACKSON 1.7329562 -0.6929937
## KANABEC 1.3646863 -0.6929937
## KANDIYOHI 1.7197950 -0.6929937
## KITTSON 1.5015319 -0.6929937
## KOOCHICHING 1.0870316 -0.6929937
## LAC QUI PARLE 1.8680899 -0.6929937
## LAKE 0.7928242 -0.6929937
## LAKE OF THE WOODS 1.6303574 -0.6929937
## LE SUEUR 1.5979922 -0.6929937
## LINCOLN 1.8260564 -0.6929937
## LYON 1.7636308 -0.6929937
## MAHNOMEN 1.4456250 -0.6929937
## MARSHALL 1.5404841 -0.6929937
## MARTIN 1.2199767 -0.6929937
## MCLEOD 1.3375197 -0.6929937
## MEEKER 1.3416955 -0.6929937
## MILLE LACS 1.2995481 -0.6929937
## MORRISON 1.2623708 -0.6929937
## MOWER 1.6294468 -0.6929937
## MURRAY 1.6253580 -0.6929937
## NICOLLET 1.7641693 -0.6929937
## NOBLES 1.6300755 -0.6929937
## NORMAN 1.3820836 -0.6929937
## OLMSTED 1.3328317 -0.6929937
## OTTER TAIL 1.5494611 -0.6929937
## PENNINGTON 1.3246513 -0.6929937
## PINE 1.0877739 -0.6929937
## PIPESTONE 1.6303984 -0.6929937
## POLK 1.5675867 -0.6929937
## POPE 1.4116740 -0.6929937
## RAMSEY 1.1995431 -0.6929937
## REDWOOD 1.7120492 -0.6929937
## RENVILLE 1.5338618 -0.6929937
## RICE 1.7205672 -0.6929937
## ROCK 1.4170797 -0.6929937
## ROSEAU 1.5982671 -0.6929937
## SCOTT 1.6981946 -0.6929937
## SHERBURNE 1.2380854 -0.6929937
## SIBLEY 1.3673371 -0.6929937
## ST LOUIS 0.8899487 -0.6929937
## STEARNS 1.4829168 -0.6929937
## STEELE 1.5389227 -0.6929937
## STEVENS 1.5520593 -0.6929937
## SWIFT 1.2574763 -0.6929937
## TODD 1.5530274 -0.6929937
## TRAVERSE 1.6938490 -0.6929937
## WABASHA 1.6642922 -0.6929937
## WADENA 1.3708520 -0.6929937
## WASECA 1.0944378 -0.6929937
## WASHINGTON 1.3404792 -0.6929937
## WATONWAN 1.9060482 -0.6929937
## WILKIN 1.5835784 -0.6929937
## WINONA 1.5716875 -0.6929937
## WRIGHT 1.5906331 -0.6929937
## YELLOW MEDICINE 1.3862294 -0.6929937
##
## attr(,"class")
## [1] "coef.mer"Unamos los coeficientes de los 3 modelos junto con los datos originales
coef_partial_pooling <-
data.frame(
county = rownames(coef(lm_partial_pooled)$county),
intercept = coef(lm_partial_pooled)$county[, 1],
coef = coef(lm_partial_pooled)$county[, 2],
modelo = "partial_pooling"
)
df_models <-
rbind(coef_pooled, coef_unpoled, coef_partial_pooling) %>%
left_join(df_mn, by = "county")Si volvemos a pintar los modelos ajustados.
p_model_comparison <- df_models %>%
filter(county %in% unique(county)[condados_num]) %>%
ggplot(aes(x = jitter(floor, factor = 0.1), y = y)) +
geom_point(size = rel(0.7)) +
geom_abline(aes(intercept = intercept, slope = coef, color = modelo)) +
facet_wrap(~county) +
labs(y = "log(radon)", x = "floor")
p_model_comparison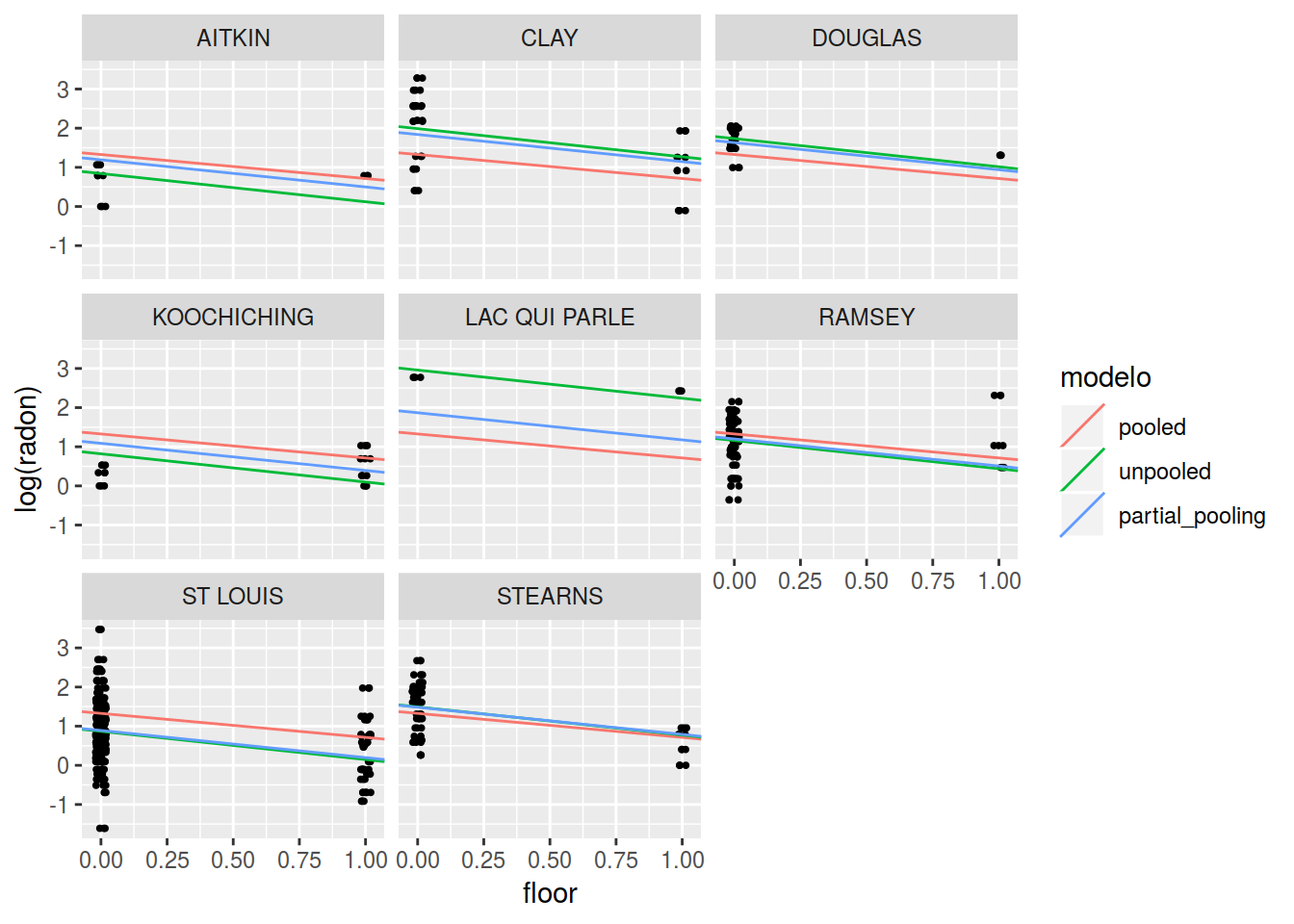
Voilá! Si nos fijamos, vemos que las estimaciones del modelo mixto representan un compromiso entre las estimaciones del modelo que no tiene en cuenta el condado y el modelo lineal que si las tiene en cuenta. En los condados dónde el modelo pooled y el no pooled eran similares el modelo mixto es similar, en los condados dónde las estimaciones eran diferentes el modelo mixto se sitúa entre ambos y si hay muchos datos se parece más al modelo no pooled mientras que si hay pocos se parece más al modelo pooled. Es decir, si hay pocos datos se parece más a lo general y si hay muchos se parece más al comportamiento particular en ese condado.